[논문 리뷰] HNSW를 위한 벡터 압축 방식 - Flash

이 글은 논문 Accelerating Graph Indexing for ANNS on Modern CPUs 을 리뷰합니다.

이번 논문은 HNSW 및 Product Quantization을 알고 있어야 이해하기 편합니다. 블로그에서 이미 다룬 적이 있으니, 익숙하지 않으신 분들은 아래 글을 먼저 읽고 오시는 것을 추천합니다.

벡터 검색 알고리즘 살펴보기(1): Similarity Search와 HNSW

벡터 검색 알고리즘 살펴보기(2): HNSW, SPANN 도 같이 읽으시면 이해하는데 HNSW를 이해할 때 도움이 됩니다. [요약] 1. FAISS는 similarity search를 도와주는 Facebook에서 만든 라이브러리다. 2. Voronoi diagram은 데이터 셋을 region으로 나누어 벡터 검색 인덱스를 만들 수 있다. 3. Product Quantization은 데이터 벡터를 압축하여 스토리지를 아낄 수 있다. Voronoi diagram과

Pangyoalto BlogPangyoalto

벡터 검색 알고리즘 살펴보기(2): HNSW, SPANN

벡터 검색 알고리즘 중 HNSW와 SPANN에 대해 알아봅니다. 들어가며 이전 “Similarity Search와 HNSW”라는 글에서 Voronoi diagram, Product Quantization, HNSW에 대해 간단히 다뤄보았다. 해당 글에서 HNSW을 자세히 다루지 못하였고 다른 ANN 알고리즘과 비교를 하지 못하여 아쉬웠었다. 이번 글은 현재 가장 많이 쓰이는 벡터 검색 알고리즘 HNSW(2016)을 살펴보고 Microsoft에서

Pangyoalto BlogPangyoalto

HNSW는 벡터 검색 알고리즘으로 가장 널리 사용되는 알고리즘입니다. HNSW 논문이 2016년에 나왔으니 어느덧 사용된지 거의 10년이 되었고, 이 알고리즘을 최적화하기 위한 여러 후속 논문들이 줄지어 나왔습니다.

이번에 다루는 Accelerating Graph Indexing for ANNS on Modern CPUs 는 SIGMOD 2025에 accept된 비교적 최근 논문입니다.

이 논문이 이전 HNSW 최적화 논문들과 다른 점은 색인에 저장되는 벡터를 압축하는 새로운 기법(Flash)을 제시했다는 점입니다. 이전 연구들은 대부분 HNSW의 알고리즘을 개선하거나 GPU 등 특화된 하드웨어에 더 잘 작동하도록 최적화하는 것이었습니다.

해당 논문은 Flash를 적용하여 벡터를 압축하면 기존 HNSW 색인에 비하여 색인 시간은 10~20배가 빨라지고 색인 크기도 2~5배 줄어든다고 밝혔습니다.

Flash는 알고리즘 수정이나 특별한 하드웨어 등을 요구하지 않아 많은 서비스에서 쉽게 사용할 수 있을 거라 생각합니다. 벡터 검색을 사용하시는 분들은 이 글을 끝까지 읽으시면 얻어가는 점들이 있을 것입니다.

Introduction: 왜 현대 CPU에서도 그래프 색인 생성은 느릴까?

벡터의 개수가 적으면 문제가 되지 않지만, 개수가 수천만에서 수억 개에 이르면 HNSW 색인 구축에만 수 시간에서 수십 시간이 걸립니다. 서비스 운영시 색인 재구축을 유저 활동이 적은 야간 시간대에 수행하더라도 벡터가 1억 개를 넘기면 하루를 넘길 수 있어 유저에게 최신 검색 결과를 보여주기 어려울 수 있습니다.

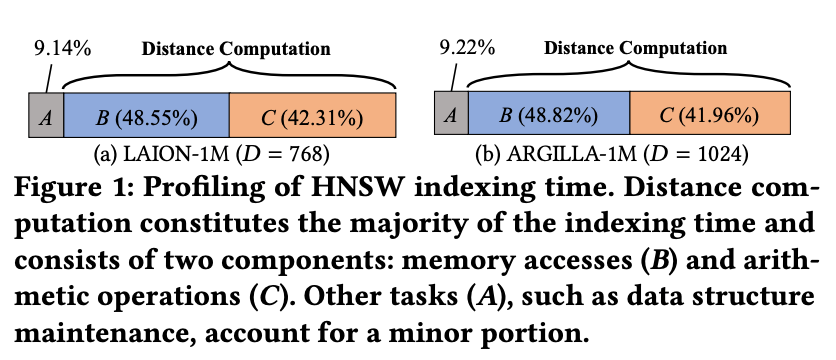
논문에서는 실제 임베딩 데이터셋에서 HNSW 색인 생성 과정을 프로파일링하여 전체 색인 시간의 약 90%가 거리 계산에 소모되고 있었고 이 중에서도 메모리 접근과 연산이 거의 반반씩 차지한다는 것을 확인했습니다.

가장 큰 원인은 두 가지입니다.

• Random memory access: HNSW 색인 내 벡터들은 메모리 상에서 spatial locality가 거의 없습니다. 따라서 거리 계산을 할 때마다 랜덤한 위치의 데이터를 불러오기에 캐시 미스가 잦습니다.
• SIMD 효율 저하: 대부분의 벡터는 768차원과 같이 고차원이고, 값은 float과 같은 4byte 타입을 가집니다.(768차원 float 벡터는 3KB의 메모리를 차지). 반면 현대 CPU의 SIMD 연산은 일반적으로 128bit(SSE)나 256bit(AVX) 단위를 처리하여, 하나의 벡터를 처리할 때 여러 번의 메모리 읽기와 연산을 나눠 수행해야 합니다. 이로 인해 SIMD의 병렬 처리 성능을 제대로 살릴 수 없습니다.

아까 앞에서 HNSW에 GPU 등을 이용한 선행 연구들을 이야기했었었는데요, 논문에서는 GPU를 이용하더라도 한계가 있다고 말합니다.

• 비용: 고성능 GPU(A100 등)는 비쌉니다.
• 메모리 제한: A100의 경우에도 10GB 메모리 한계로 수백 기가바이트 크기의 벡터셋 전체를 다루기 어렵습니다.
• 엔지니어링 복잡도: GPU 병렬화를 위한 전용 코드 작성과 유지 관리가 필요합니다.

현실적으로 이러한 이유들로 대부분의 벡터 검색 시스템에서는 CPU 기반으로 운영해야하지만 기존 방식으로는 성능에 한계가 있었습니다.

문제 분석 - 거리 계산

앞에서 HNSW 색인 생성의 병목은 거리 계산에서 발생하는 것을 확인했습니다. 논문에서는 거리 계산의 어떤 과정이 병목인지 분석합니다.

표기(Notation)
- 각 벡터는 x, y 같은 볼드체 소문자로 표현됩니다.
- 두 벡터 간 유클리드 거리는 𝛿(x, y)로 표기합니다.
- 집합은 X, C(x) 같은 볼드체 대문자로 나타냅니다.

HNSW 색인 생성은 크게 두 단계로 나뉩니다.

1. Candidate Acquisition (CA)
2. Neighbor Selection (NS)

Candidate Acquisition (CA)

CA는 새로운 벡터를 색인에 넣을 때, 이와 가까운 후보 벡터들을 찾는 과정입니다. 이때 HNSW는 greedy search를 수행합니다.

그래프에는 벡터 값이 아니라 이웃들의 ID만 저장되어 있기 때문에, 실제 거리 계산을 하려면 매번 메모리에서 벡터 데이터를 불러와야 합니다. 여기서 random memory access가 발생합니다.

Neighbor Selection (NS)

NS는 CA에서 모은 후보들 중 실제로 연결할 이웃을 고르는 단계입니다. 후보들 간 거리도 계산해야 하고, 입력된 벡터와의 거리도 다시 비교합니다. 이 과정 역시 벡터 데이터를 랜덤하게 접근하게 됩니다.

CA와 NS 두 단계 모두에서 random memory access가 반복되며, 이때 발생하는 캐시 미스와 메모리 레이턴시가 성능을 크게 저하시킵니다.

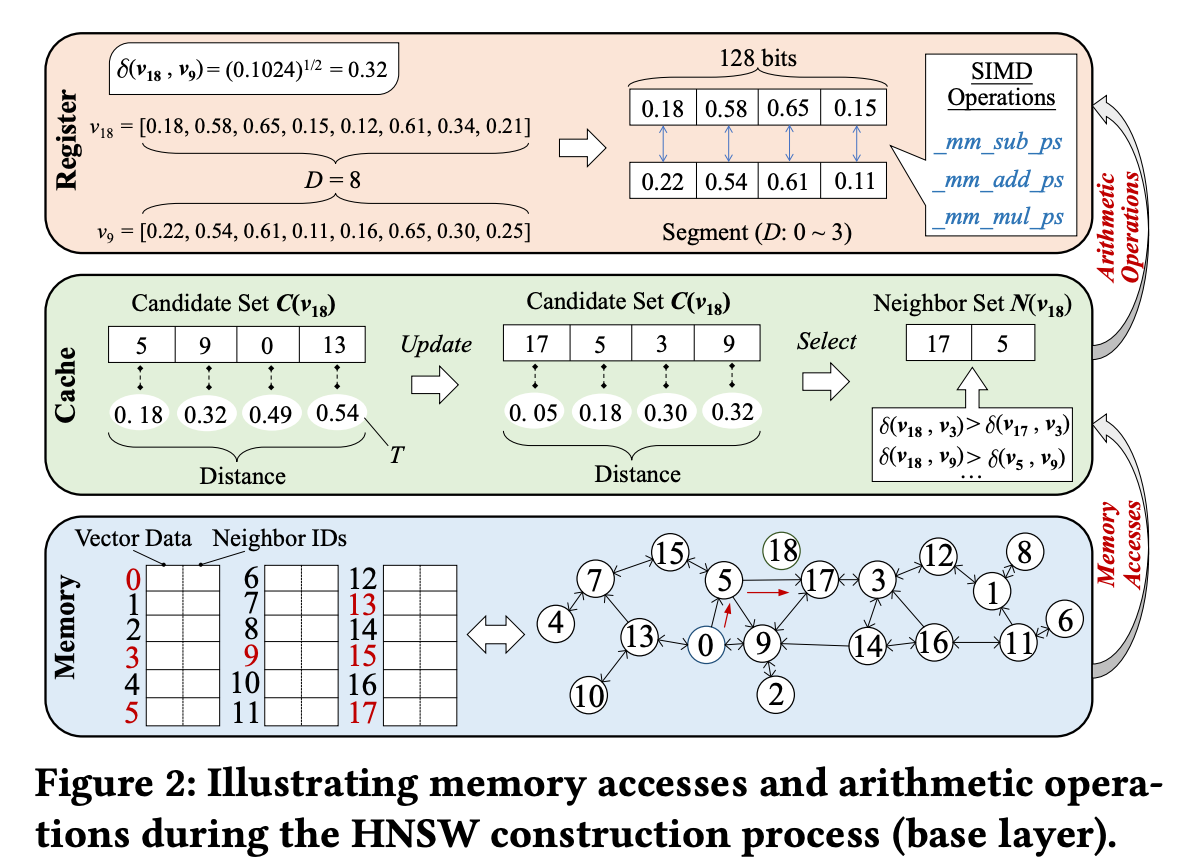
Figure 2를 보면서 색인 생성 예를 따라가볼까요.

Figure 2는 벡터 v₁₈을 그래프에 삽입하는 과정을 나타냅니다. 여기서 후보 집합 크기 C는 4, 최종 이웃 수 R은 2로 가정합니다.

CA 단계

1. v₁₈ 삽입 시, 벡터 v₀부터 탐색 시작
2. v₀의 이웃들을 확인하고, 그들과의 거리를 계산해 초기 후보 집합 C(v₁₈) = {v₅, v₉, v₀, v₁₃} 형성
3. 가장 먼 거리인 𝛿(v₁₈, v₁₃) = 0.54를 threshold T로 설정
4. 이후 가장 가까운 이웃 v₅로 이동, 이웃들을 다시 조사
5. 새 후보들 간 거리 계산 후 T보다 작은 것만 남겨 업데이트
6. 최종 C(v₁₈) = {v₁₇, v₅, v₃, v₉}

NS 단계

1. 가장 가까운 v₁₇이 먼저 선택
2. 𝛿 (𝒗17, 𝒗3) < 𝛿 (𝒗3, 𝒗18), 𝛿 (𝒗17, 𝒗9) < 𝛿 (𝒗9, 𝒗18) 이므로 거리 비교 결과 v₃, v₉가 제거됨 (HNSW에서 최종 candidate를 정하는 휴리스틱)
3. 최종적으로 v₅, v₁₇이 v₁₈과 연결됨

CA 및 NS 단계를 진행하면서 접근하는 벡터들은 메모리에 랜덤하게 퍼져 있습니다. 그림 하단의 메모리 레이아웃을 보면, 후보로 선택된 벡터들이 서로 멀리 떨어져 있는 걸 알 수 있습니다. 이로 인해 캐시 미스가 반복됩니다.

벡터를 압축해도 거리 비교를 정확하게 할 수 있을까

이 논문은 기존의 PQ(Product Quantization), SQ(Scalar Quantization), PCA와 같은 벡터 압축 기법들을 바탕으로 새로운 압축 방법을 설계합니다.

벡터 압축을 적용하려면압축한 벡터의 거리 비교 결과가 원본 벡터의 거리 비교 결과와 같아야 합니다.

벡터를 압축해도 거리 비교를 정확하게 할 수 있다

논문은 HNSW 색인 과정의 거리 계산을 두 가지로 나눕니다.

• DC1: 후보를 업데이트할 때의 거리 계산
• DC2: 최종 이웃을 고를 때의 거리 계산

논문에서는 새로 들어온 벡터 u와 기존 벡터 v, w 사이의 거리 비교 결과가 압축했을 때도 동일하려면 어떤 조건을 만족해야하는지 제시합니다.

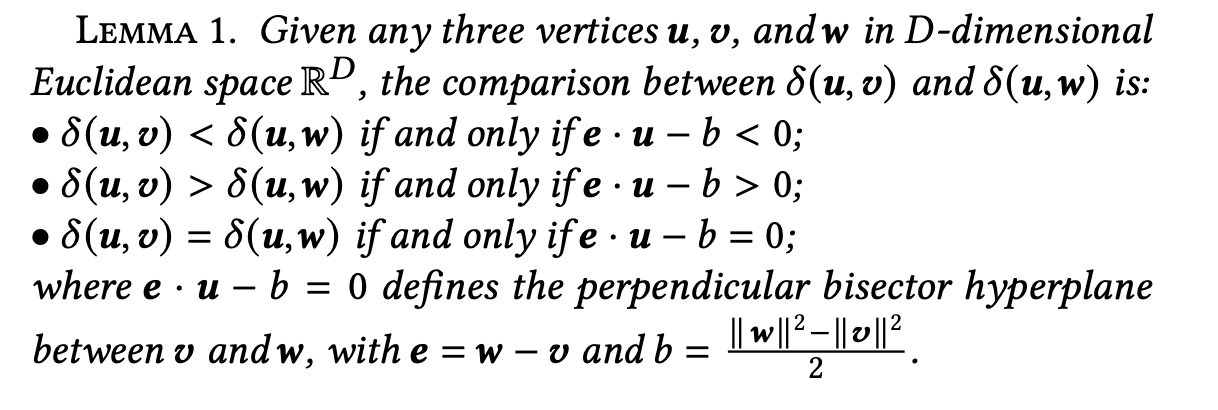
논문은 Lemma 1을 통해 거리 비교를 대체할 수 있는 다른 방법을 소개합니다. (증명은 논문 참고)

세 벡터 u, v, w가 있을 때 다음을 만족합니다.

• 𝛿(u, v) < 𝛿(u, w) ⇔ e·u − b < 0
• 𝛿(u, v) > 𝛿(u, w) ⇔ e·u − b > 0
• 𝛿(u, v) = 𝛿(u, w) ⇔ e·u − b = 0

여기서 e = w − v, b = (‖w‖² − ‖v‖²) / 2 입니다.
즉, 복잡한 유클리드 거리 계산 없이 내적 연산 하나로 비교가 가능하다는 뜻입니다.

이를 DC1, DC2에 적용하면 다음과 같습니다:

• DC1: candidate set을 업데이트할 때, e·u − b > 0이면 w를 후보로 포함시킵니다.
• DC2: neighbor를 고를 때, 후보 u를 제거할지 여부도 e·u − b로 판단합니다.

즉, 거리 비교 전부를 e·u − b > 0 하나로 통일할 수 있습니다.

논문은 Theorem 1을 통해 벡터가 압축되었을 때 사용할 수 있도록 확장을 합니다. (증명은 논문 참고)

Theorem 1에 따르면 압축된 벡터들 u′, v′, w′를 사용할 경우에도, |e·u − b| ≥ |E|라는 조건만 만족하면 거리 비교 결과가 그대로 유지됩니다.

여기서 E는 압축 오차 값입니다(정의는 위 Theroem 1 참고). E를 정의할 때 사용하는 Eₓ는 압축 과정에서 생긴 에러 벡터로 Eₓ = x − x′로 정의됩니다.

이를 통해 우리가 알 수 있는 것은 압축 오차 값만 통제하면 벡터 압축을 사용할 수 있다는 것입니다.

압축 파라미터 찾기

논문은 적절한 압축 파라미터를 찾기 위해 다음과 같은 실험을 하였습니다.

1. 데이터셋에서 임의의 1만 개 벡터 샘플링
2. 각 벡터마다 가장 가까운 이웃 100개를 찾고, 그 중 2개를 골라 triple (u, v, w) 구성
3. 각 triple마다 압축 후 벡터 u′, v′, w′ 생성
4. 그리고 각 triple에 대해 |e·u − b|와 |E|를 계산
5. 이때 |e·u − b| ≥ |E|를 만족하면서, 벡터 크기를 최소로 하는 압축 파라미터를 최종 선택

뒤에 논문이 제시하는 압축 방식 Flash를 소개할 때 여러 하이퍼 파라미터들이 나옵니다. 다만 하이퍼 파라미터를 어떻게 설정해야 적절하게 작은 |E|를 얻을 수 있는지 나와있지는 않습니다.

적절하게 하이퍼 파라미터를 설정하면 |E|가 충분히 작게 나와 벡터 검색시 압축을 사용해도 괜찮다 정도로 이해해도 넘어가도 괜찮을 것 같습니다. 실제로 Flash 평가 부분을 보면 충분한 Recall이 나옵니다.

Flash: 새로운 벡터 압축 기법

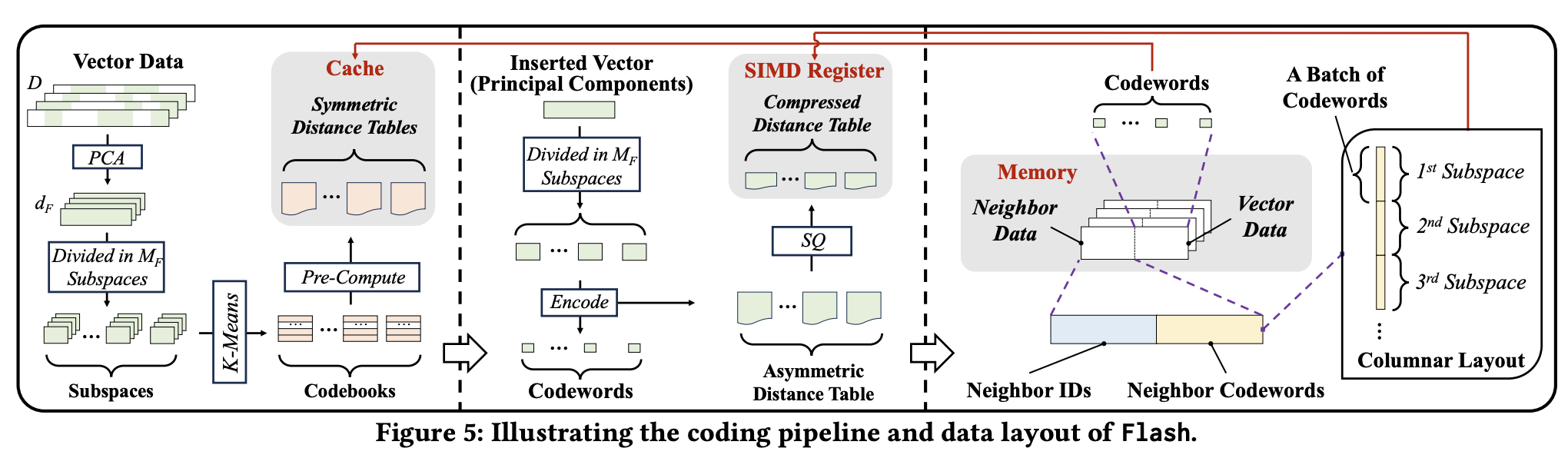
논문이 제시한 새로운 압축기법 Flash는 PQ, SQ, PCA에 영감을 받았으며 특히 PQ의 기법을 레버리지한 방법입니다.

핵심 아이디어는 고차원 벡터를 여러 서브스페이스로 나누고, 각 서브스페이스를 병렬로 처리하는 것입니다.

CPU는 여러 개의 SIMD 레지스터를 병렬로 사용할 수 있습니다. Flash는 이를 이용합니다.

• 고차원 벡터를 여러 서브스페이스(subspace)로 분할
• 각 서브스페이스는 하나의 레지스터에 대응되도록 구성
• 거리 계산 시, 각 레지스터가 서브스페이스별 partial distance를 병렬로 계산

ADT & SDT

Flash는 두 가지 타입의 distance table을 생성합니다.

ADT (Asymmetric Distance Table)

• CA 단계에서 사용
• SQ(Scalar Quantization)로 압축되어 레지스터에 바로 로딩 가능
• SIMD 연산 효율 향상, 레지스터 읽기 최소화

SDT (Symmetric Distance Table)

• NS 단계에서 사용
• 캐시에 저장

이 두 테이블은 각각의 벡터를 압축해 표현할 때 할당할 비트 수를 최적화합니다.

하이퍼 파라미터

Flash는 두 개의 주요 하이퍼파라미터를 가집니다.

• 서브스페이스 개수 (MF)
• principal component 차원 (dF)

이 파라미터들은 색인 생성 속도와 검색 정확도 사이의 트레이드오프를 조절합니다. 하지만 SIMD 정렬이나 메모리 접근 패턴 자체에는 영향을 주지 않습니다.

PCA

서브스페이스 단위로 압축을 하려면, 차원 간 분산이 고르게 분포되어야 좋습니다. 하지만 실제 임베딩 데이터는 특정 차원에 정보가 몰려 있는 경우가 많습니다.

그래서 Flash는 PCA(주성분 분석)을 사용합니다.

• 벡터 데이터들로 centered matrix 계산
• centered matrix로 공분산 행렬(covariance matrix) 계산
• 고유값(λ, eigen value) 계산

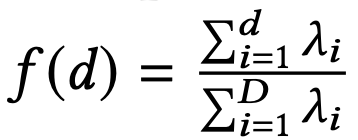
함수 f(d)를 정의하고, f(d) ≥ α가 되는 최소 차원 dF를 principal component 차원으로 설정합니다.

이렇게 얻은 basis로 벡터의 데이터 차원을 줄이면서 정보 손실을 최소화할 수 있습니다.

위 PCA 부분은 PCA를 잘 모르시다면 이해가 어려울 수 있습니다.
뒷 내용은 PCA를 몰라도 이해에 어려움은 없습니다.

Subspace Division and Distance Table Compression

Flash는 SIMD 효율을 극대화하기 위해 고차원 벡터를 서브스페이스 단위로 나눕니다.

PCA를 적용한 후, 압축된 벡터는 다음과 같이 서브벡터들로 구성됩니다.

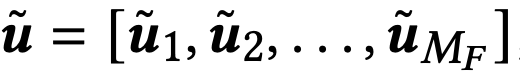
Flash는 PQ과 유사하게 각 서브스페이스 i에 대해 codebook Ci​를 구성합니다.

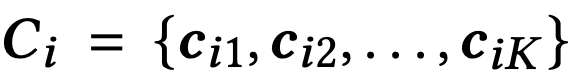
• cij:  i번째 서브스페이스의 centroid
• K: centroid 개수 (codeword 개수)

각 서브벡터 ui는 아래 식을 통해 가장 가까운 centroid로 매핑됩니다.

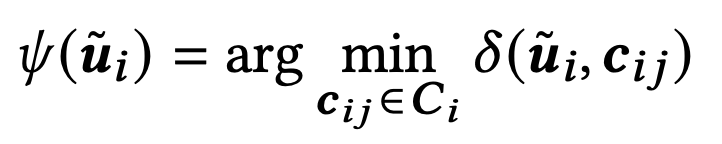
결과적으로 하나의 벡터는 MF​개의 codeword로 표현됩니다. 각 codeword는 K개의 centroid를 표현할 수 있어야 하므로 log₂K 비트를 차지합니다.

ADT: Asymmetric Distance Table

각 입력 벡터에 대해 Flash는 ADT를 생성합니다. ADT는 ui​와 codebook Ci​의 모든 centroid 간 거리 계산을 저장해둔 테이블입니다.

ADT를 미리 계산해두면 CA(Candidate Acquisition) 단계에서 입력 벡터와 기존 노드 간의 거리를 빠르게 계산할 수 있습니다.

하지만 SIMD에 최적화하려면 거리값을 그대로 저장하면 안 됩니다. Flash는 Scalar Quantization (SQ)을 적용해 아래와 같이 거리값을 Quantization 합니다.

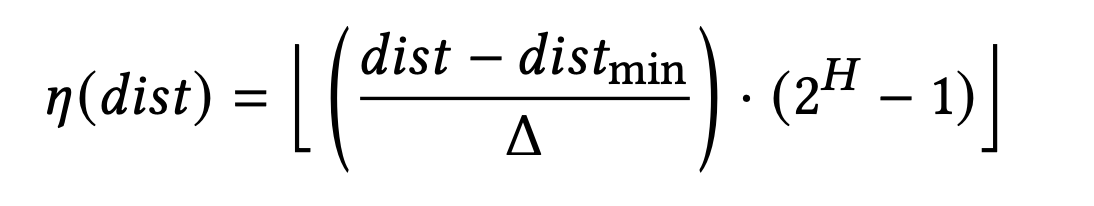
• 𝜂(𝑑𝑖𝑠𝑡) : quantized distance
• Δ :  quantization step size (Δ = 𝑑𝑖𝑠𝑡𝑚𝑎𝑥 − 𝑑𝑖𝑠𝑡𝑚𝑖𝑛)
• H : quantized distance를 담을 수 있는 비트 개수

예를 들어, K=16, H=8이라면, ADT는 총 128bit로 표현되고, 이는 하나의 SIMD 레지스터에 딱 맞게 들어갑니다.

ADT는 입력 도중 레지스터 내 일차원 배열로 존재하다가, 입력이 끝나면 해제됩니다.

SDT: Symmetric Distance Table

NS(Neighbor Selection) 단계에서는 ADT 대신 SDT가 사용됩니다.

SDT는 각 서브스페이스에서 codeword들끼리의 거리 정보를 저장합니다. 즉, centroid 간의 distance들을 미리 계산해놓는 것입니다.

• 총 MF개의 SDT가 생성 (서브스페이스마다 있어야 하므로)
• 각 SDT는 K * K 개의 거리 값 포함
• 캐시에 2차원 배열로 저장

Access-Aware Memory Layout

일반적인 HNSW 색인 구조는 모든 벡터가 고정된 크기의 neighbor 리스트를 갖고 메모리 상에서 각 벡터의 위치는 vertex ID로 계산됩니다. 즉, 벡터 ID로 offset을 계산해서 해당 위치에 접근합니다.

문제는 neighbor 벡터들이 너무 커서 ID와 함께 연속적으로 저장하기 어려워 random memory access가 발생합니다.

Flash는 ID + codeword를 저장함으로써 이를 해결했습니다. 각 vertex의 neighbor 리스트는 다음과 같이 구성됩니다.

• 고정된 크기의 메모리 블록에 neighbor ID들을 저장
• 그 옆에 각 neighbor의 codeword들을 순서대로 저장

이렇게 하면 그래프 탐색 시 벡터 전체를 읽지 않고도 codeword만으로 거리를 계산할 수 있어 random access 없이도 거리 계산이 가능해집니다. 그 뿐만 아니라 SIMD 연산에 딱 맞게 정렬됩니다.

SIMD

ADT는 이미 각 서브스페이스별 거리값을 quantized된 형태로 SIMD 레지스터에 저장하고 있습니다. Flash는 SIMD 연산에서 이 ADT를 참조해 거리를 계산합니다.

• 한 번의 연산에서 B개의 neighbor codeword를 SIMD 레지스터로 로드
• codeword 값은 ADT에서 partial distance를 가리키는 index 역할
• SIMD의 shuffle operation을 사용해 index 순서대로 레지스터 값을 재정렬

이 방식은 다음 장점들이 있습니다.

• branch 없이 처리 가능
• 추가 메모리 접근 없이 ADT에서 바로 거리값 추출 가능
• 매우 빠름 (레지스터 내 연산이므로)

SIMD 연산으로 계산된 각 서브스페이스의 partial distance들을 합하여 최종 거리를 계산합니다. 이 합연산 역시 SIMD로 처리됩니다.

ADT 참조는 SIMD shuffle 연산을, 거리 합산은 SIMD add 연산을 사용함으로써 Flash는 단순히 데이터 압축뿐만 아니라 SIMD에 연산 흐름을 맞추어 재설계하였습니다.

HNSW + Flash

Flash는 기존 HNSW 구조에 자연스럽게 통합될 수 있도록 설계되었습니다.

구현 과정은 크게 preprocessing → index 생성 → 거리 계산으로 나뉩니다.

1. Preprocessing: PCA와 Codebook 생성

먼저 데이터셋에서 principal component를 추출합니다.

• 데이터셋 일부를 샘플링
• PCA로 principal components 추출
• 각 서브스페이스에 대해 codebook 생성
• centroid 간 거리 정보를 기반으로 SDT(Symmetric Distance Table) 생성

2. Index 생성: codeword 변환 & ADT 구성

색인을 생성할 때 각 벡터 u는 다음 과정을 거칩니다.

• PCA를 통해 압축된 후, 여러 서브벡터 ui​로 분할
• 각 서브벡터는 codebook Ci​에 대해 가장 가까운 centroid로 매핑됨
• 매핑 결과로 codeword들이 생성됨 (각 codeword는 log₂K 비트 크기)

이때 ADT (Asymmetric Distance Table)는 다음 방식으로 구성됩니다:

• 각 ui​와 Ci​ 내 centroid 간 거리 계산
• 거리값들은 SQ(Scalar Quantization)를 통해 quantized
• 완성된 ADT는 SIMD 레지스터에 저장되어 입력이 끝날 때까지 유지

3. 거리 계산: ADT & SDT 사용

색인 생성 중, Flash는 두 가지 방식의 거리 계산을 수행합니다.

• 벡터 u ↔ neighbor batch 거리 계산 → ADT 사용
• candidate ↔ candidate 거리 계산 → SDT 사용

ADT는 SIMD-friendly 형태로 저장돼 있어 빠른 batch 거리 계산이 가능하고 SDT는 candidate 간 거리를 빠르게 판별하는 데 활용됩니다.

4. 하이퍼파라미터 설정

• MF​: 서브스페이스 개수
• dF​: principal component 차원.
• LF: codeword 비트 수
• B: batch 크기

MF와 dF는 압축 에러 조정에 사용됩니다.

LF와 B는 SIMD 레지스터 크기에 따라 설정됩니다.

비용 분석

(1) Candidate Acquisition (CA) 단계

기존 HNSW

시간 복잡도: O(R⋅log⁡n)

• R: 최대 neighbor 수
• log⁡n: 탐색 경로의 평균 길이

각 hop마다 neighbor들의 벡터 데이터에 접근해 메모리 random access가 발생합니다

Flash 적용

시간 복잡도: O(log⁡n)

Flashs는 neighbor들의 ID + codeword를 연속된 메모리 블록에 저장하여 벡터 전체를 로드하지 않아도 codeword만으로 거리 계산이 가능합니다. 이를 통해 random memory access를 제거하였습니다.

추가적으로, Flash는 벡터를 압축했기 때문에 데이터 크기 자체도 작아져 캐시 히트율이 증가합니다.

(2) Neighbor Selection (NS) 단계

NS에서는 candidate 간 거리 비교가 반복됩니다.

기존 HNSW

• 각 candidate 간 비교 시 벡터 데이터를 매번 로딩
• 메모리 접근 횟수: O(C), C는 candidate set 크기

Flash 적용 시

• 벡터 접근 없음
• 모든 거리 정보는 SDT (Symmetric Distance Table)에 미리 저장되어 있고 L1 캐시에 올라갈 정도로 작습니다. L1 캐시에 올라갔다면 메모리 접근 0회가 가능합니다.

(3) SIMD 기반 거리 계산의 메모리 로드 횟수

기존 HNSW

로드 횟수: 32 * D / U

• 32: float 비트 수
• D: 벡터 차원
• U: SIMD 레지스터 비트 width

Flash 적용 시

로드 횟수: MF * H / U

• MF: 서브스페이스 개수
• H: 각 서브스페이스당 quantized distance 비트 수

D=768, U=128, MF​=16, H=8 가정시 SIMD 로드 횟수 192배 감소

평가(Evaluation)

논문에서는 파라미터를 다음과 같이 세팅하였습니다.

• C (candidate 최대 수): 1024
• R (neighbor 최대 수): 32

일반적인 HNSW와 HNSW에 PCA, SQ, PQ, Flash를 사용해 벡터를 인코딩했을 때를 비교하였습니다.

(1) 색인 생성 시간

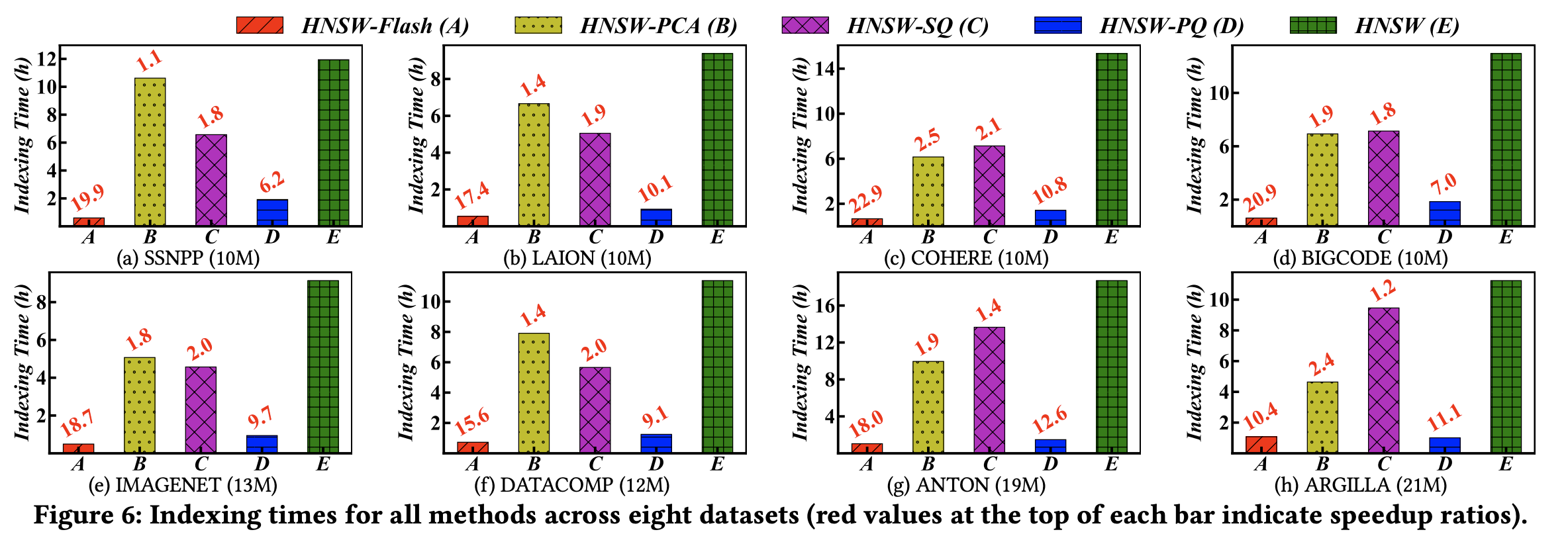
색인 생성 시간에는 인코딩을 위한 데이터 처리 시간도 포함되어 있습니다.

HNSW-Flash가 HNSW에 비하여 10~20배 정도 색인 생성 시간이 빠릅니다. 다른 압축 기법 대비해서도 훨씬 뛰어난 성능을 보입니다.

(2) 색인 크기

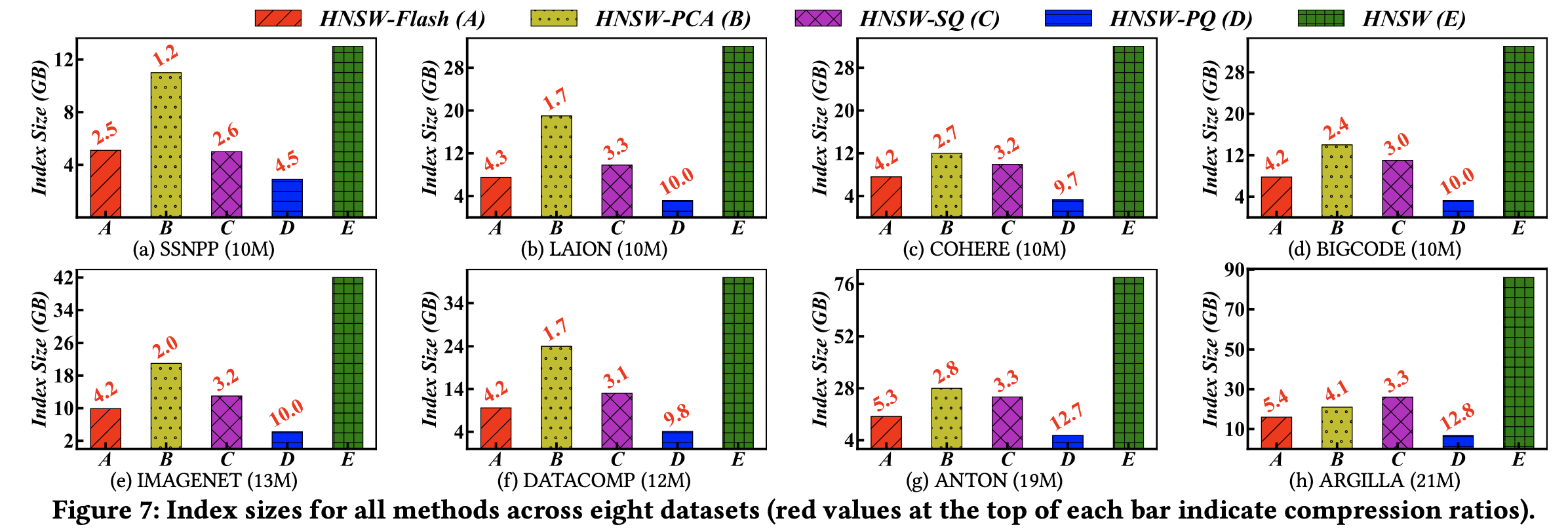
Flash를 적용했을 때 적용하지 않았을 때보다 색인 크기가 2~5배 정도 작아지는 것을 확인할 수 있습니다.

(3) qps - recall

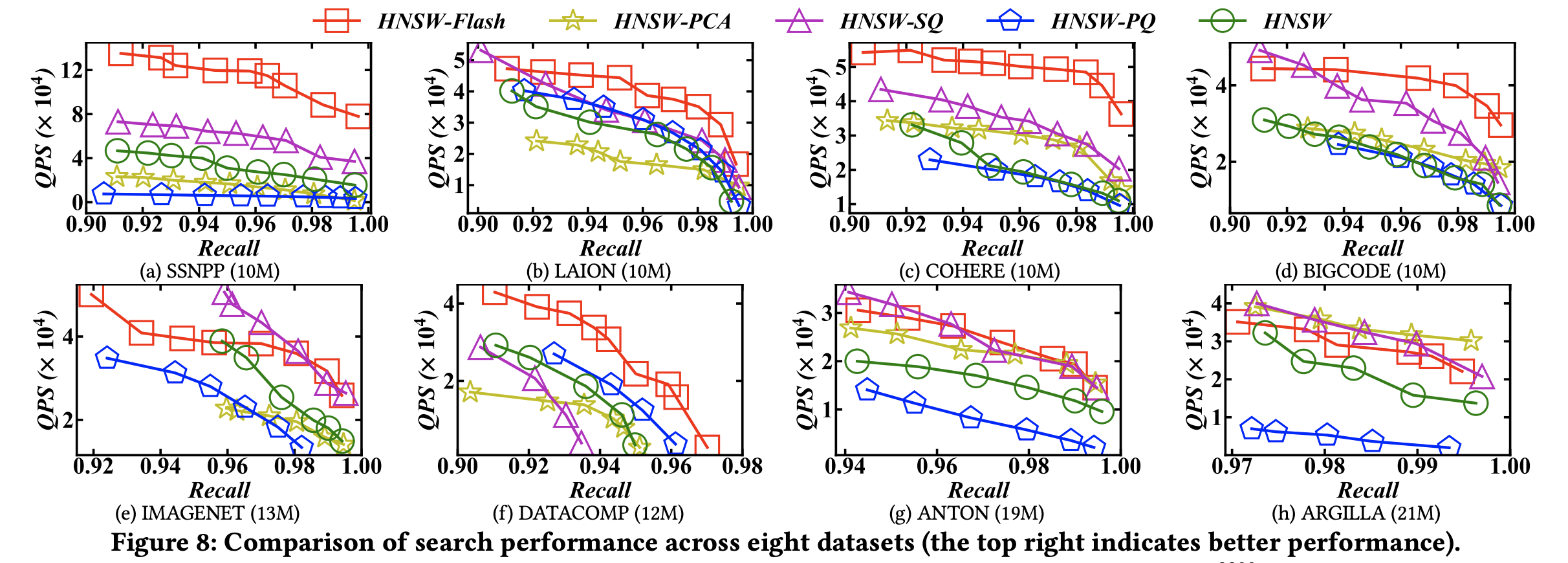
Flash를 사용했을 때 다른 기법들 대비하여 동일한 Recall 기준 높은 QPS를 기록하는 것을 확인할 수 있습니다.

(4) Flash 사용시 색인 생성 시간 분석

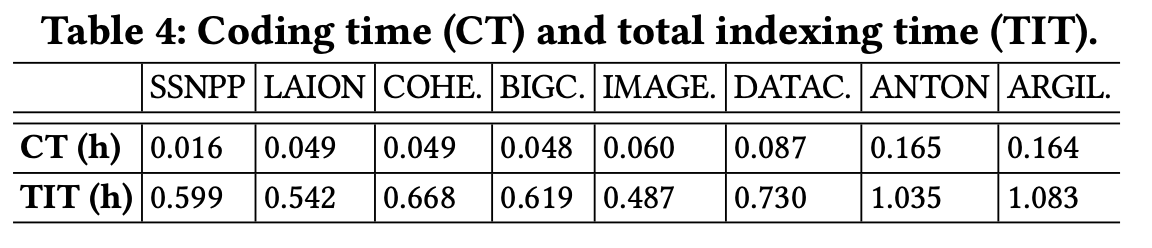
Flash를 사용했을 때 색인 생성 시간을 분석해보면 Coding Time은 전체 색인 생성 시간에서 약 10% 정도를 차지하는 것을 확인할 수 있습니다.

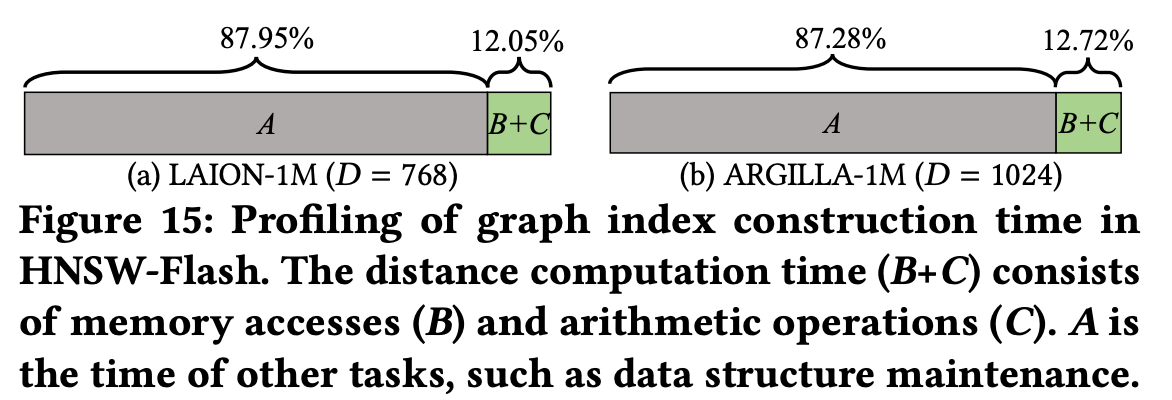
Flash 적용 후 기존 색인 생성 시간의 병목으로 지적되었던 거리 계산 시간 + 메모리 접근 시간은 전체 색인 생성 시간의 12%로 비중이 감소하였습니다.

(5) 하이퍼 파라미터

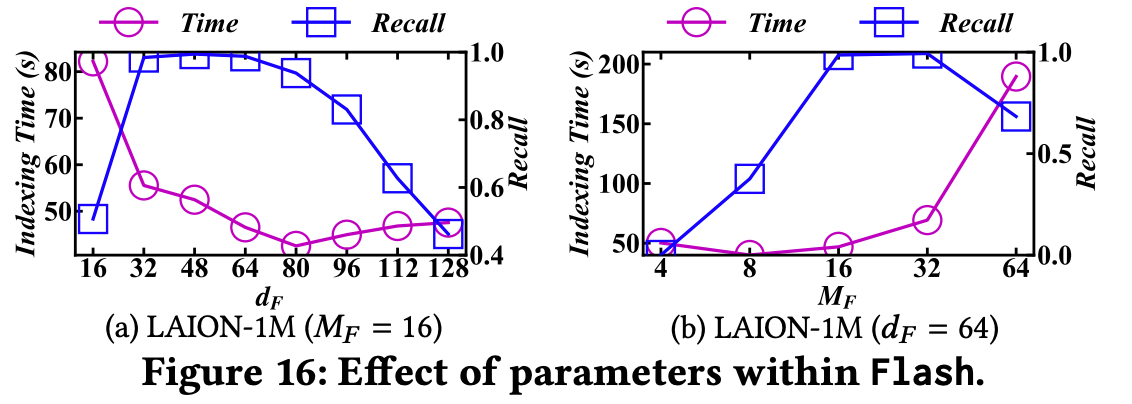
dF (principal component 차원)과 MF(서브 스페이스 개수)는 색인 생성 효율성과 색인의 퀄리티에 영향을 미칩니다.

위 그림을 참고하면 최적의 값은 MF 16과 dF 64입니다.

나의 생각

서비스 적용 전 생각해봐야할 점

(1) HNSW 색인에 벡터를 증분으로 입력시 성능이 떨어질 염려가 있다

Flash 구현을 살펴보면 전체 벡터 데이터셋에 대하여 PCA를 적용하여 전체 차원 개수를 줄이고 basis를 생성합니다. 이 basis들로 벡터들의 차원을 줄이는 것입니다.

또한 PQ(Product Quantization)을 통해 벡터의 서브 스페이스들을 양자화하는데, 이 또한 벡터 데이터셋에 대해 수행합니다.

한번에 배치로 HNSW 색인을 생성하면 이는 아주 적합한 방법입니다.

하지만 만약에 이미 만든 HNSW 색인에 새로운 벡터를 증분으로 넣는다면 새로 입력된 벡터는 제대로 압축이 되지 않을 수 있습니다(정보 손실 발생 가능). 왜냐하면 PCA와 PQ는 이미 존재하는 데이터셋에 대해 최적화가 되어 있기 때문입니다.

그렇기에 HNSW 색인에 증분 벡터 입력을 많이 한다면 recall이 떨어질 수 있습니다.

(2) PCA, PQ를 하는 것이 부담이 될 수 있다

Flash는 벡터를 색인에 입력 하기전 PCA와 PQ를 적용을 미리 합니다.

입력할 벡터마다 적용을 하는 것이 아니라, 전체 데이터셋에 대해 한번에 수행해야 하기 때문에 어플리케이션 입장에서는 부담이 될 수 있습니다.

느낀 점

개인적으로 HNSW 코드를 변경하지 않고 적용할 수 있다는 점에서 마음에 드는 논문이었습니다. 많은 서비스에서 시도를 해볼 수 있는 논문이라고 생각합니다.

논문에서 제시한 압축 방법(Flash)는 단순히 압축을 하는 것에서 그치지 않고 SIMD 연산에 최적화하기 위해 ADT와 SDT를 생성하고 이를 적극적으로 활용하는 것이 굉장히 치밀하게 설계되었다고 느꼈습니다.

치밀한 설계를 가지고 있음에도 Flash를 이해하는 것이 그렇게 어렵지 않아(PCA, PQ 등을 이미 알고있다면) 굉장히 좋은 알고리즘이라고 생각했습니다.

Flash에 사용된 아이디어는 나중에 HNSW를 넘어 새로운 벡터 검색 알고리즘이 나오더라도 사용할 수 있을 것 같아 논문을 완전히 이해하고 넘어가면 좋을 것 같습니다.

벡터 검색을 사용하고 계시다면 Flash 사용을 고려해보는 것을 추천합니다. 저자가 직접 구현한 소스코드도 존재합니다.

Reference

Accelerating Graph Indexing for ANNS on Modern CPUs

Flash Github