벡터 검색 알고리즘 살펴보기(1): Similarity Search와 HNSW

벡터 검색 알고리즘 살펴보기(2): HNSW, SPANN 도 같이 읽으시면 이해하는데 HNSW를 이해할 때 도움이 됩니다.
[요약]
- FAISS는 similarity search를 도와주는 Facebook에서 만든 라이브러리다.
- Voronoi diagram은 데이터 셋을 region으로 나누어 벡터 검색 인덱스를 만들 수 있다.
- Product Quantization은 데이터 벡터를 압축하여 스토리지를 아낄 수 있다. Voronoi diagram과 같이 사용할 수 있다.
- NSW는 ANN 검색시 사용하는 graph 자료구조다. Skip list는 검색과 입력이 평균 O(logn) 복잡도를 가지는 자료구조이다.
- HNSW는 Skip List의 아이디어를 NSW에 적용시킨 것으로 데이터 셋의 크기가 커져도 좋은 검색 성능을 유지한다.
- HNSW과 Voronoi diagram을 같이 사용하면 Voroni centroid의 개수를 많이 유지할 수 있다. 따라서 Inverted File Index로 Voronoi diagram 단독 사용보다 더 좋은 성능을 낸다.
[목차]
- FAISS가 뭔데?
- Voronoi diagrams
- Product Quantization
- NSW, Skip List
- HNSW - Hierarchical Navigable Small World graphs
이 글은 벡터 검색 라이브러리 FAISS에 대한 시리즈의 첫번째 글입니다. Similarity Search 및 FAISS의 핵심 인덱스인 HNSW에 대해 설명합니다.
1. FAISS가 뭔데?
FAISS는 Facebook에서 만든 벡터 클러스터링 및 similarity search 라이브러리이다. Similarity search는 어떤 쿼리 벡터가 들어왔을 때 기존에 가지고 있는 벡터 셋과 거리를 계산해 유사한 벡터들을 검색하는 것이다. 여기서 두 벡터가 유사하다는 것은 두 벡터간 거리가 가깝다는 의미이며, 벡터간 거리를 계산하는 방법은 유클리드 거리, 맨해튼 거리 등 여러 가지가 있다.
FAISS는 가장 가까운 벡터 검색은 물론 k번째 가까운 벡터 검색, 배치로 여러 벡터들을 한번에 검색하기 등 여러 기능들을 보유하고 있다. 이러한 기능들 덕분에 대표적인 벡터 데이터베이스 Milvus의 경우 FAISS를 확장해 사용하고 있다.
이번 글은 FAISS에서 지원하는 인덱스 중 하나인 HNSW(Hierarchical Navigable Small World graphs)을 살펴볼 것이다. HNSW는 ANN(approximate nearest neighbors) 검색에서 가장 널리 사용되고 성능이 좋은 SOTA 알고리즘이다. HNSW을 먼저 살펴보기 전, Similarity search에 대한 기초 지식들을 먼저 살펴본 뒤 HNSW가 어떻게 동작하는지 분석할 것이다.
2. Voronoi diagram

Voronoi diagram은 주어진 데이터 셋을 가까운 데이터끼리 모아 region을 나눈 것을 말한다. 한 cell 안에 속한 데이터는 다른 cell보다 해당 cell과의 거리가 제일 가깝고, Cell을 나누는 선은 두 cell과 같은 거리에 있다. 또한 Voronoi diagram의 각 cell은 자신의 중앙을 가르키는 centroid를 가진다.
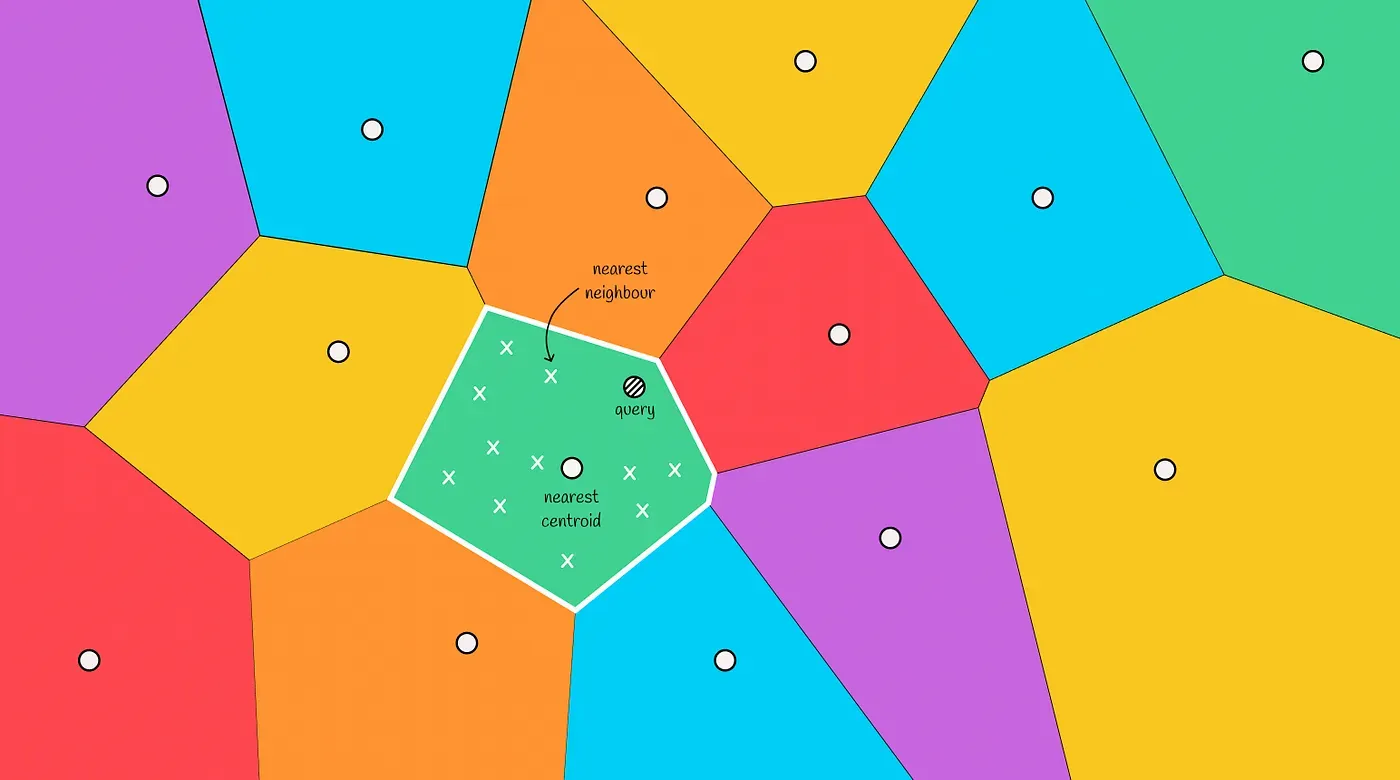
새 데이터가 주어지면 모든 voronoi 파티션의 centorid로부터 거리를 계산한다. 이렇게 계산된 거리 중 가장 짧은 거리를 가진 centroid의 cell은 새 데이터와 유사하다고 판단할 수 있다.
따라서 Voronoi diagram을 사용하면 similarity search을 구현할 수 있다. 쿼리 벡터가 속할 cell의 벡터들이 다른 cell의 벡터보다 가까울 것이기 때문이다.
Voronoi diagram의 각 centroid를 미리 저장하면 벡터 검색의 역색인으로 사용할 수 있다. 역색인이 없다면 쿼리 벡터가 들어왔을 때 모든 벡터와 거리 계산한 이후 가장 가까운 벡터를 찾아야 한다. 하지만 미리 Voronoi diagram을 만들었다면 Centroid와의 거리를 먼저 계산하고 가장 가까운 centroid의 cell에 속한 벡터들만 검색 대상으로 설정할 수 있다. 모든 벡터가 아닌 특정 cell의 벡터들만 거리를 계산하기 때문에 검색 속도가 크게 향상된다.
하지만 가장 가까운 cell의 벡터들의 거리만 계산하는 것은 검색된 벡터가 쿼리 벡터와 가장 유사하다는 것을 보장하지 못한다. 쿼리 벡터가 두 cell의 경계 근처에 있는 경우에는 다른 cell에 있는 벡터가 오히려 가장 가까울 수도 있기 때문이다. 따라서 가장 가장 가까운 centroid만 조사하는 것이 아닌 m개의 centroid를 조사하는 방법도 있다.
정리하면 Voronoi Diagram을 사용해 Inverted File을 적용하면 쿼리 벡터와 비슷한 벡터들을 빠르게 찾을 수 있다.
3. Product quantization
벡터의 개수가 많아지면 거리 계산시 메모리가 이슈가 될 수 있다. 따라서 벡터의 데이터 압축을 하면서 거리 계산에도 문제가 없는 방법이 필요하다.
Product quantization은 각 데이터 벡터를 short memory-eifficient representation(PQ 코드라고 함)로 변경하는 작업이다. Product quantization은 lossy-compression 방법이라 검색 정확도를 낮출 수 있지만, 실제 사례에서 잘 작동한다.
Product quantization 인코딩 알고리즘
- 각 벡터를 동등하게 서브벡터로 나눈다.
- 모든 데이터셋의 벡터는 독립적인 서브 스페이스를 생성한다.
- 클러스터링 알고리즘은 각 서브 스페이스에서 수행된다. 이를 통해 각 서브 스페이스에서 여러 centroid가 생성된다.
- 서브 스페이스의 centroid를 quantized vector라고 한다.
- 클러스터 ID를 reproduction value라고 한다.
- 각 서브 벡터는 자신이 소속된 centroid의 ID로 인코딩된다.
- 추가적으로 모든 centorid의 coordinate는 나중에 사용되므로 저장해놓는다.
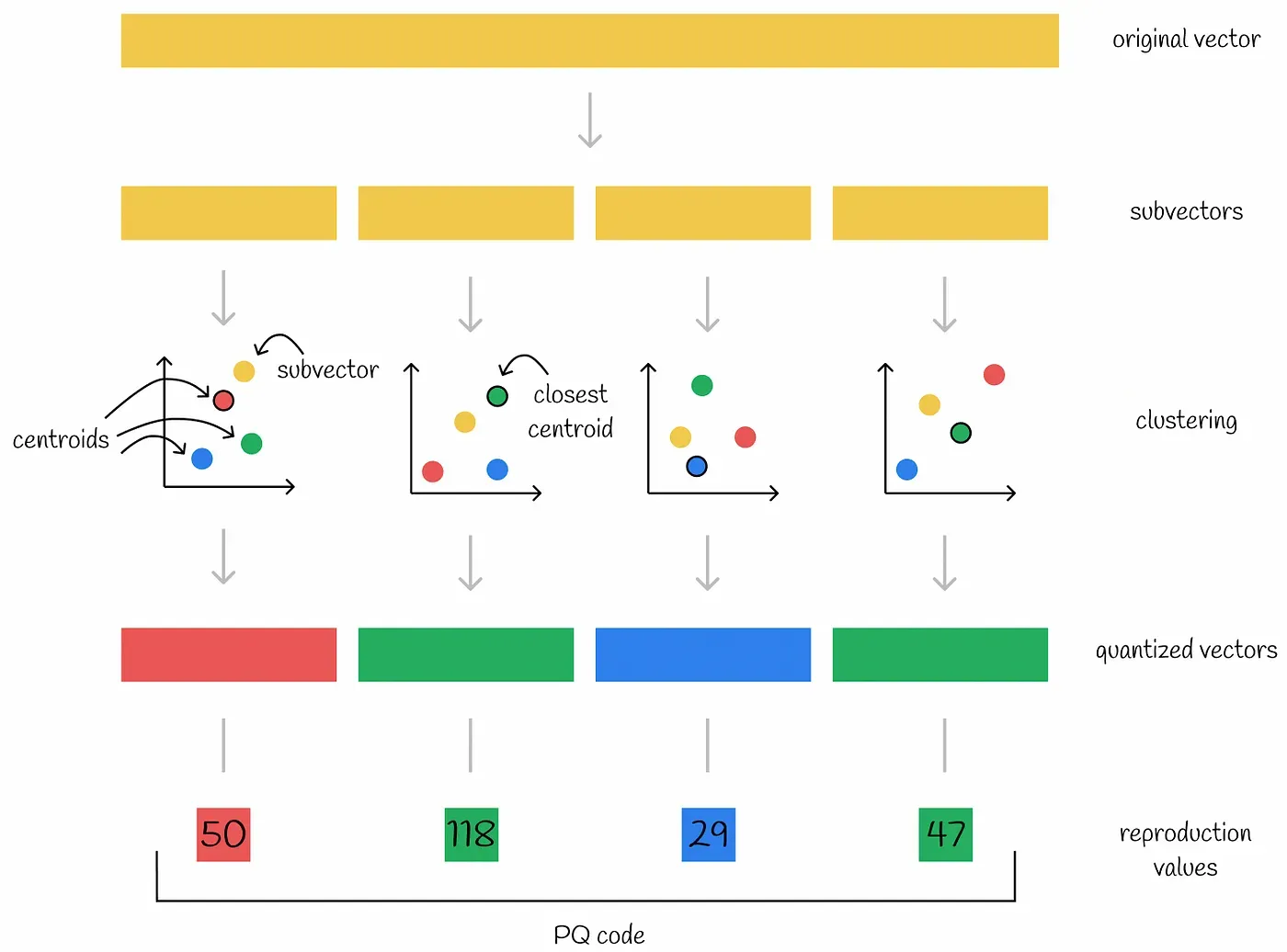
원본 벡터가 n개의 서브 벡터로 나뉘면 n개의 숫자(각 서브 벡터의 centroid ID)로 인코딩을 할 수 있게 된다. 즉, 원본 벡터의 각 부분이 서브 벡터와 가장 가까운 centroid id로 인코딩되는 것이다. 예를 들어 위 그림에서 인코딩된 벡터 50 118 29 47은 첫번째 서브 벡터와 가까운 centroid는 50, 두번째 서브 벡터와 가까운 centroid는 118, 세번째 네번째 centroid는 29와 47이라는 뜻이다.
보통 centorid의 개수(k)는 2의 거듭 제곱으로 잡는다. 각 서브벡터에 m개의 비트를 쓴다고 하면 나타낼 수 있는 최대 centroid id는 2^m이기 때문이다. 따라서 인코딩된 벡터를 저장하는데 사용하는 메모리는 n*log(k) 비트가 된다.
예시로 32비트 float를 1024개 가지고 있는 벡터를 살펴보자. 해당 벡터를 8개의 서브 벡터로 나누고 각 서브벡터가 centroid가 256개인 클러스터(k=256)로 인코딩하면 얼마나 저장공간을 아낄 수 있을까?
- original : 1024 * 32 = 4096 byte
- encoded: 8 * 8 = 8byte
무려 500배 이상의 압축 효과를 가져옴을 알 수 있다. 원본 서브 벡터가 아닌 가까운 centroid의 벡터를 이용하기 때문에 원래 벡터의 정확한 값을 복원할 수는 없다. 하지만 클러스터의 개수를 늘리면 실제 어플리케이션에 쓸 수 있을 정도의 정확도를 유지하면서 스토리지는 크게 아낄 수 있다.
Product quantization Inference
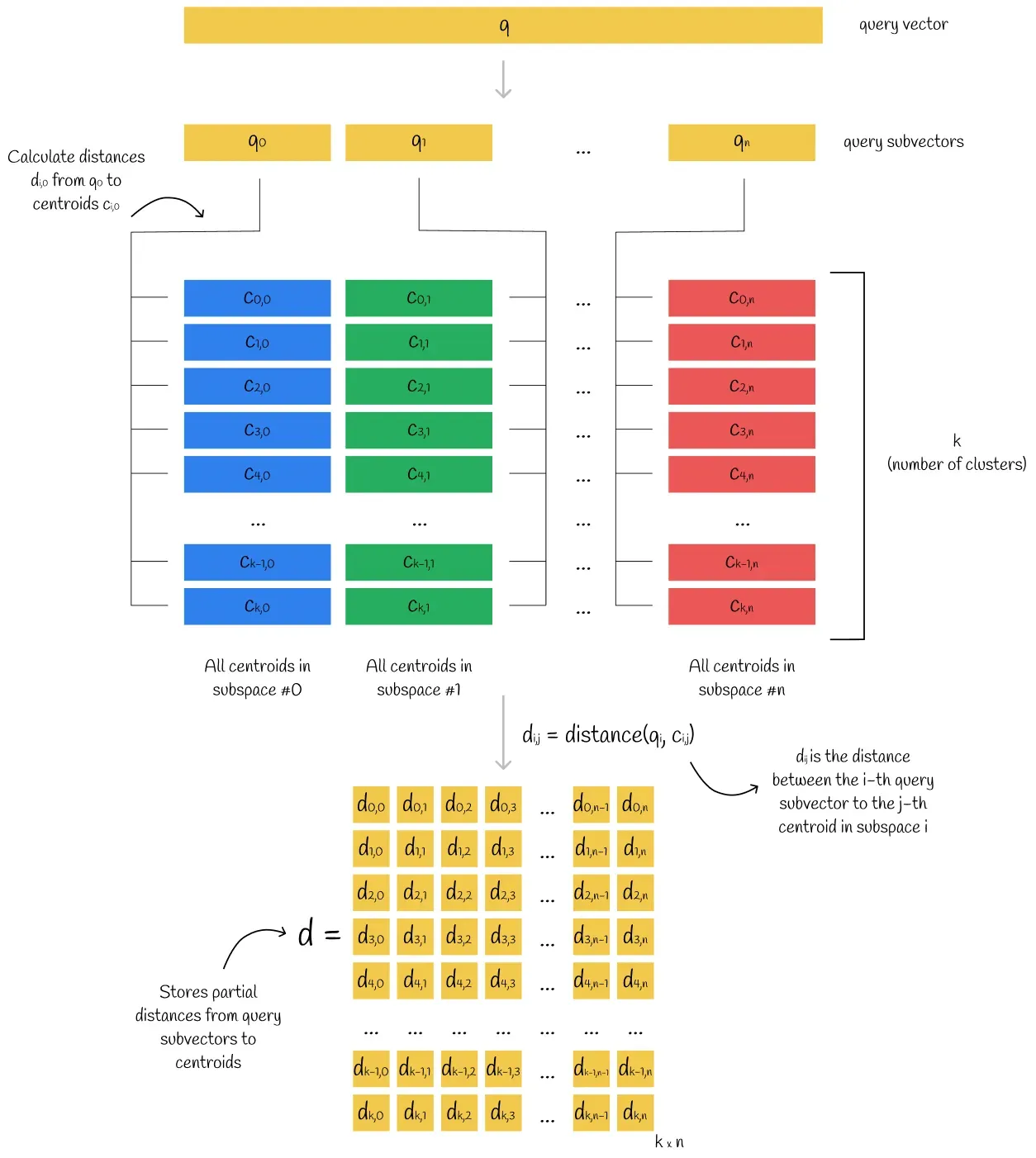
어떤 쿼리 벡터와 인코딩된 벡터의 거리는 쿼리의 서브 벡터와 인코딩된 벡터의 centroid와의 거리를 계산하여 산출해낼 수 있다. 모든 인코딩된 벡터의 서브 스페이스는 같은 centroid들을 공유한다. 따라서 쿼리 벡터와 서브 스페이스의 centroid들과의 거리를 미리 계산하면 어떤 인코딩된 벡터와의 거리를 빠르게 계산할 수 있다. 이를 위해 쿼리 벡터를 여러 서브 벡터로 나누고, 각 서브 벡터에 대응되는 서브 스페이스의 모든 centroid 거리를 계산해 테이블 d에 담는다(서브벡터와 centroid의 거리는 partial distance라고 불린다).
테이블 d를 이용해 쿼리 벡터와 특정 벡터와의 approximate distance를 계산하는 방법은 아래와 같다.
- 벡터의 서브 벡터마다 가장 가까운 centroid j를 찾는다. 그리고 그 centroid와 쿼리 서브벡터 i와의 partial distance d[i][j]를 테이블 d로부터 가져온다
- 모든 partial distance를 square하고 sum한다.
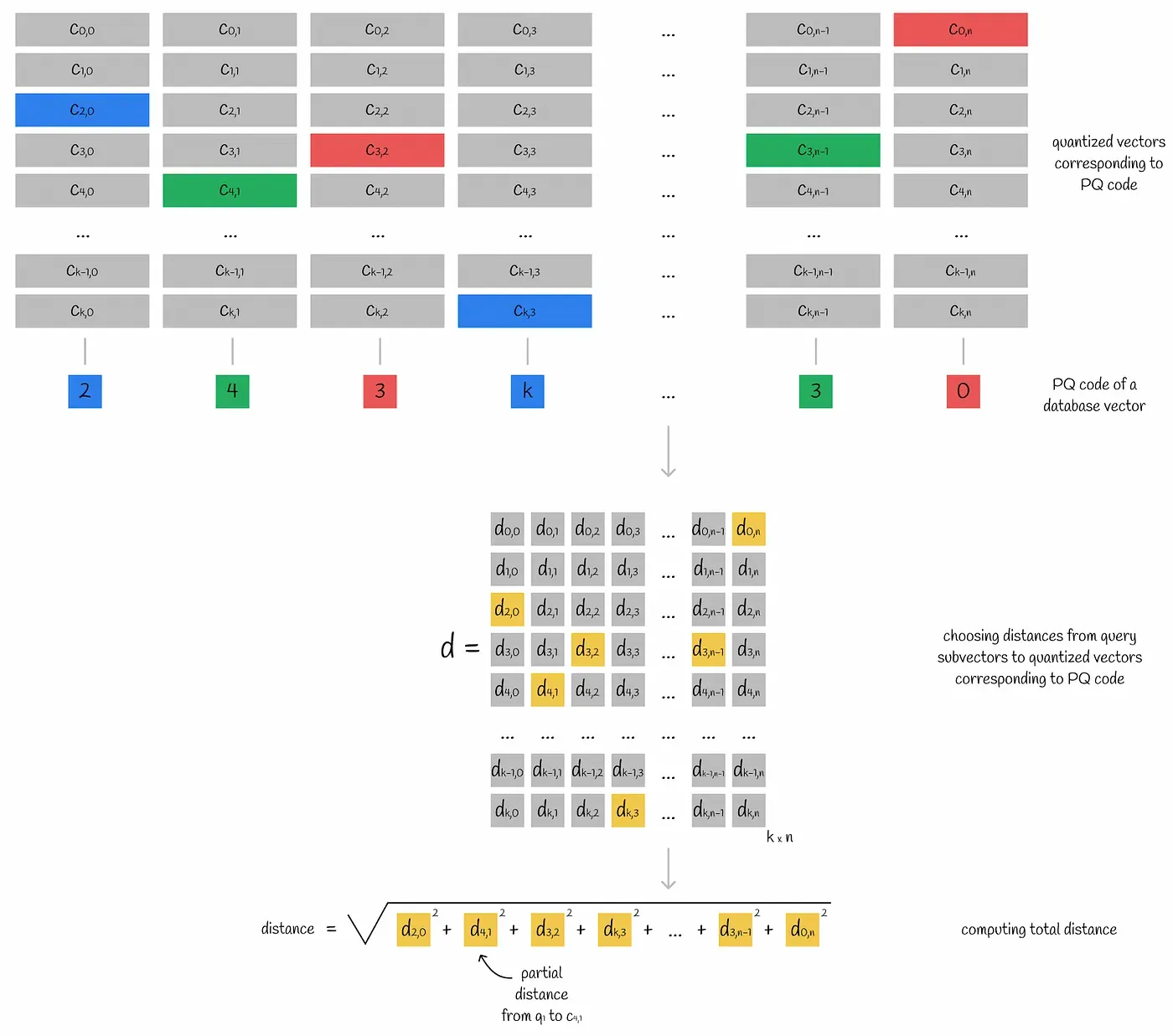
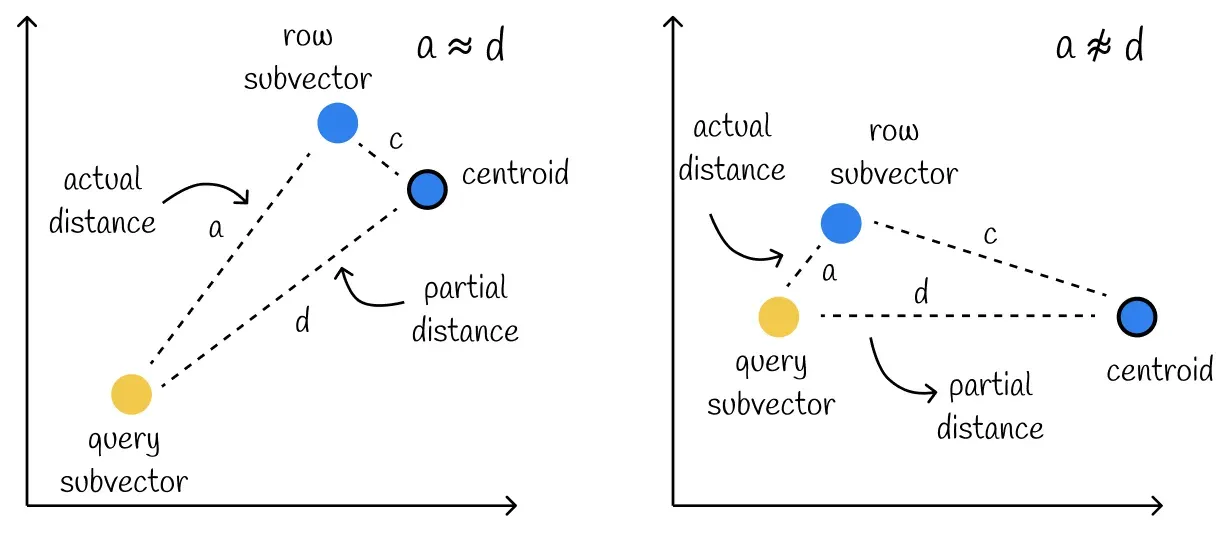
이렇게 만들어진 partial distance d는 실제 거리 a와 상당히 유사하다.
다만 아래의 케이스와 같이 centroid와 서브벡터의 거리가 멀 때 정확도가 떨어지는 케이스도 존재해 결과가 부정확하게 나올 수도 있다.
Product quantization을 사용하면 압축이 상당히 잘 되고, 특정 어플리케이션에선 95% 이상 압축된다.
다만 트레이드 오프로 각 서브 스페이스의 quantized vector들을 담고 있는 사이즈 k*n 크기의 메트릭스 d를 저장해야 하고, 각 DB 벡터들마다 k*n의 partial distance를 브루트 포스로 계산해야 한다.
Product quantization과 Voronoi diagram
Voronoi diagram에 Product quantization을 적용할 때 residual 벡터를 사용한다.
Residual 벡터는 centroid로부터 벡터까지의 offset이다. 즉, centroid와의 차이다.
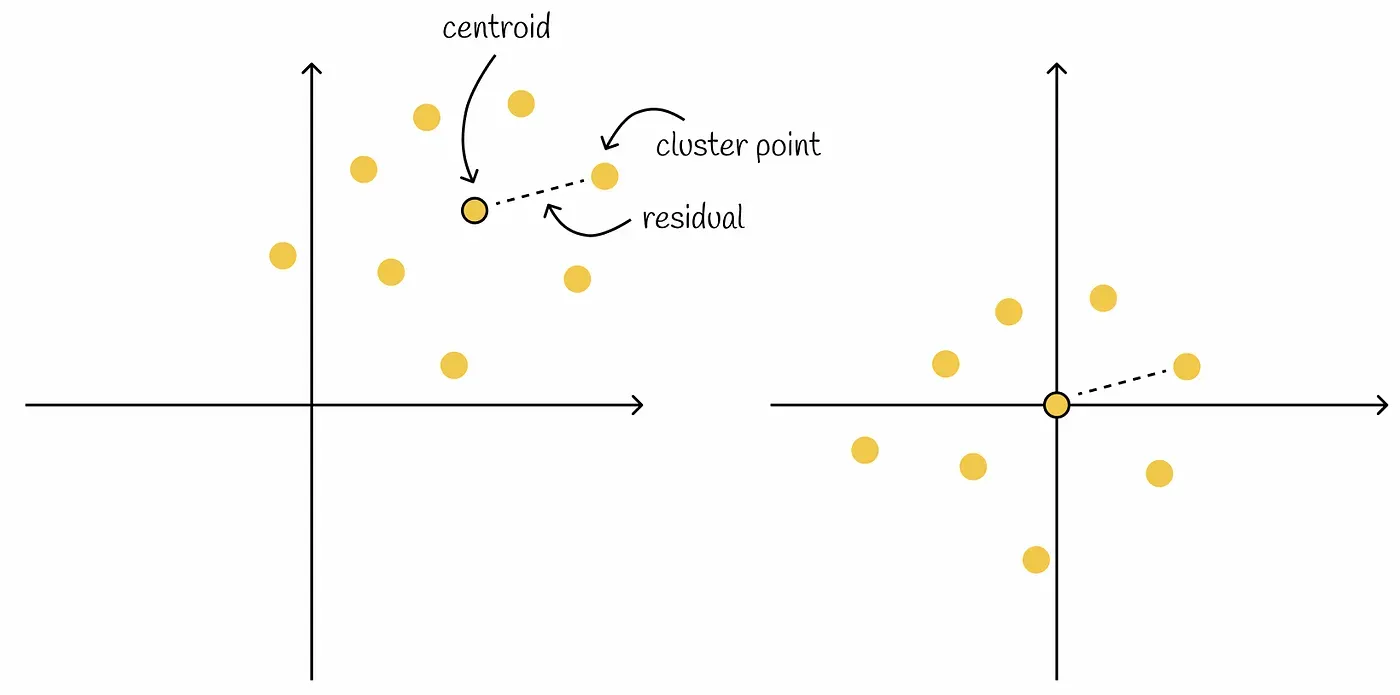
왼쪽 그림의 벡터들에서 centroid를 다 빼면 우측 그림처럼 변경된다. 다만 모든 클러스터의 벡터가 동일하게 움직였기에 벡터간 relative distance는 변경되지 않는다.
두 클러스터가 존재하는 경우 아래와 같이 클러스터마다 residual을 다르게 표시할 수 있다.
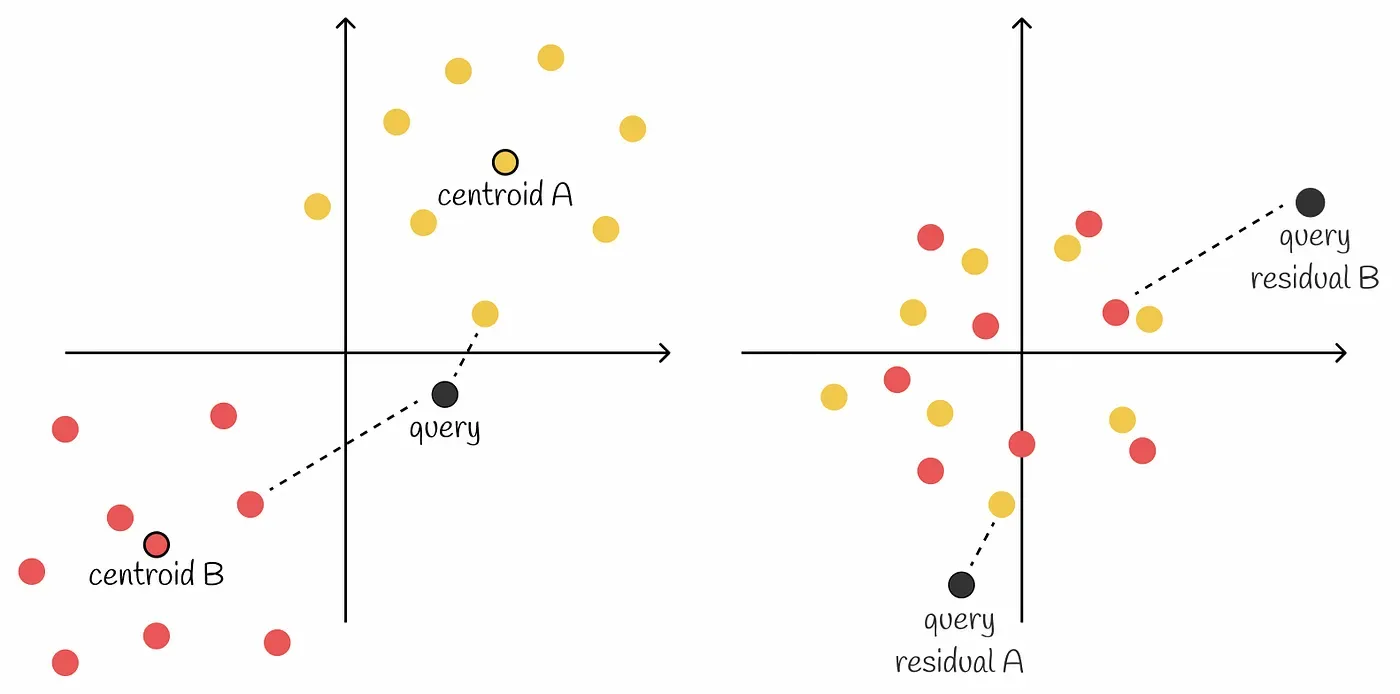
알고리즘
- 주어진 벡터 DB에 대해 벡터들을 n개의 Voronoi 파티션으로 나눈다.
- 각 Voronoi partition의 벡터들에 centroid를 빼면 벡터들은 0 주변으로 모이게 된다. 원본 벡터는 centroid 벡터와 residual만 저장만 있으면 복구가 가능하다. 따라서 원본 벡터를 따로 저장할 필요 없다.
- 각 파티션의 모든 벡터들에 대해 product quantization을 수행한다.
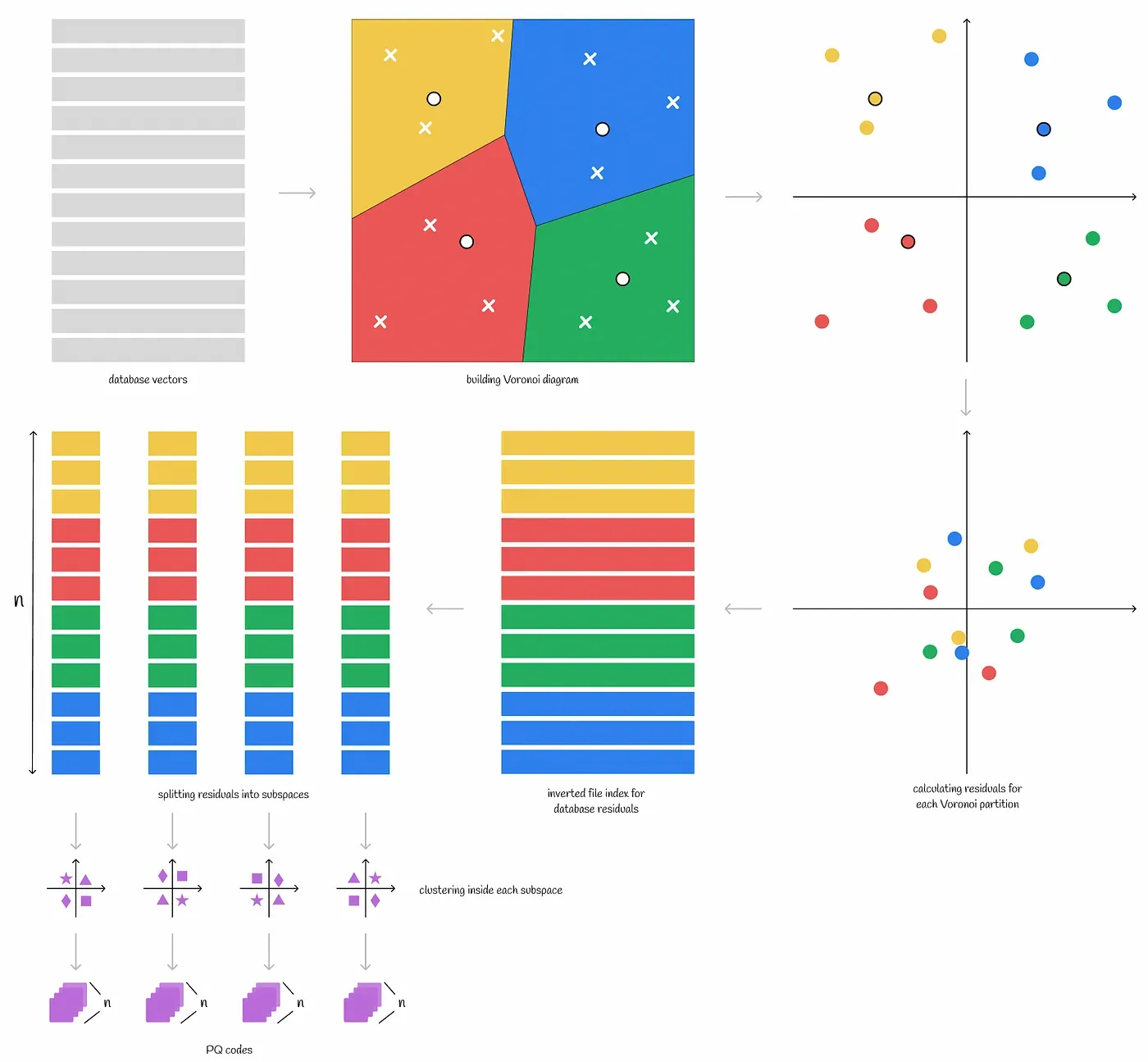
residual로 벡터들을 저장하면 파티션으로 나누었음에도 벡터들이 서로 겹치게 된다. 즉, 이전과 비교하여 같은 길이의 PQ 코드를 사용했을 때 벡터를 더 정확하게 표현할 수 있게 된다. 벡터를 표현할 때 더 적은 값들을 사용할 수 있기 때문이다.
Voronoi diagram + Product quantization의 Inference
앞서 원본 벡터는 centroid 벡터와 residual만 저장만 있으면 복구가 가능해 원본 벡터를 저장하지 않는다고 했었다. 그래서 검색시 쿼리 벡터도 residual 벡터로 변환하여 거리를 계산해야 한다.
- 주어진 벡터와 가까운 k개의 Voronoi 파티션 centroid를 찾는다.
- 각 파티션들의 residual을 가져와 residual 벡터들과 거리를 계산한다.
- 2의 거리 계산 방법은 product quantization 알고리즘처럼 쿼리 residual을 서브 벡터들로 나누고 matrix d를 만든 뒤 거리를 계산하는 것이다.
우리는 similarity search에서 인덱스를 할 수 있는 Voronoi diagram과 데이터 압축 방법인 Product quantization을 살펴보았다. 이제 ANN의 SOTA 알고리즘인 HNSW및 이를 Vornoi diagram과 어떻게 같이 사용할 수 있는지 알아볼 것이다.
3. Skip List, NSW
HNSW(Hierarchical Navigable Small World)는 Skip List와 NSW(Navigable Small World)로부터 영향을 받았다. HNSW을 살펴보기 전 Skip List와 NSW를 먼저 살펴보자.
Skip List
Skip list는 검색과 입력이 평균 O(logn) 복잡도를 가지는 확률적 자료구조다. 원소들을 정렬된 상태로 유지하여 검색이 용이하면서 링크드 리스트와 비슷한 형태를 가지고 있어 입력 역시 유리하다.
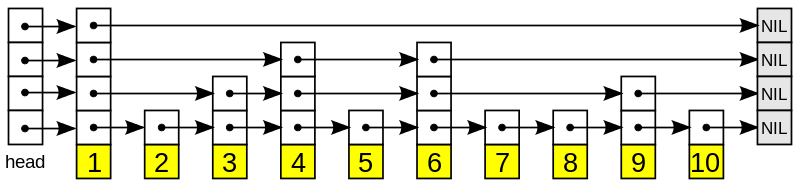
Skip list는 여러 레이어로 이루어져 있고, 가장 아래 레이어는 일반적인 링크드 리스트이다. i번째 레이어에 등장하는 원소는 i+1번째 레이어에 확률적으로 등장한다.
이 확률 값을 p라고 하면 각 원소들은 평균 1/(1-p)개의 레이어에 등장하고 가장 키가 큰 원소는 모든 레이어에 등장한다. Skip list는 base가 1/p인 logn개의 레이어를 가지게 된다.
Skip List의 검색
- 검색은 가장 상단의 레이어부터 이루어진다.
- 현재 보고 있는 원소가 타겟 원소보다 크거나 같을 때까지 전진한다.
- 현재 보고 있는 원소가 타겟 원소보다 크다면 이전 원소로 되돌아간 뒤 아래 레이어로 이동한다.
검색 복잡도는 O(logN)인데, 이 복잡도를 유도하는 과정은 아래와 같다.
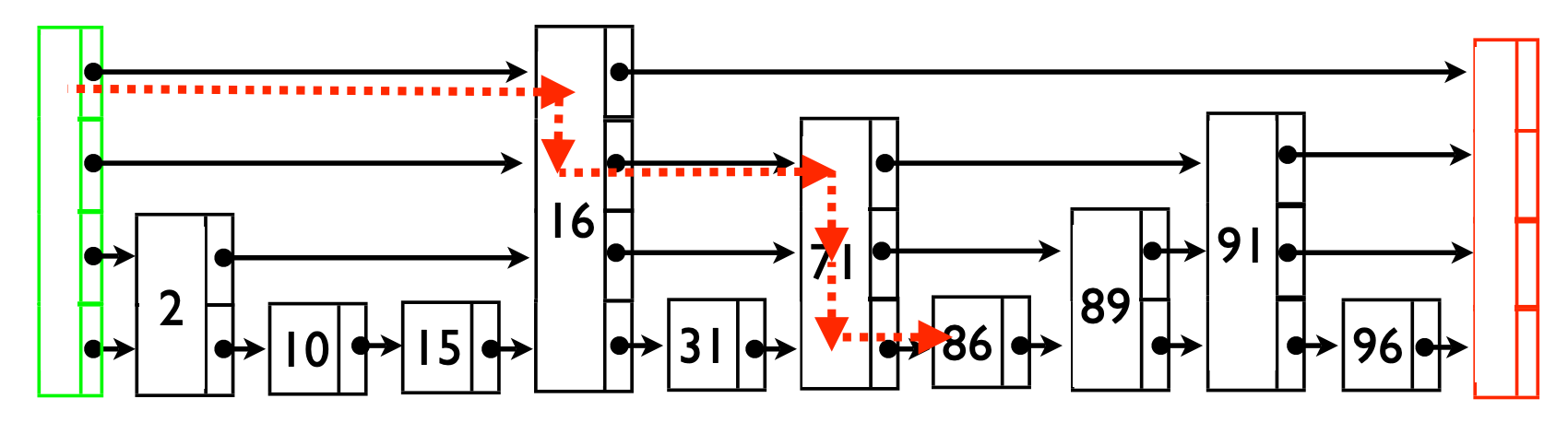
어떤 타겟 원소 k를 찾기 위한 경로를 반대 순서로 분석해보자. 경로에 있는 원소가 여러 레이어에 속해 있으면 가장 위에 있는 레이어까지 올라가는 것이 최적의 경로다.
따라서 경로를 반대로 올라가 j레벨까지 가는데 소모되는 스텝 기댓값 C(j)라고 하면 C(j) = 1 + p*C(j-1) + (1-p)*C(j) 이다. 한 스텝을 소모했을 때 j-1레벨로 갈 확률이 p, 아닐 확률이 1-p이기 때문이다. 즉 C(j) = 1/p + C(j-1)이기 때문에 각 레이어에서 평균적으로 1/p 개의 스텝을 소모한다.
전체 레이어 개수 기댓값은 base가 1/p인 logN이므로 검색 시간은 O(logN) 복잡도이다.
NSW(Navigable Small World)
Navigable Small World는 long range edge와 short range edge를 가지고 있는 proximity graph이다.
Navgiable Small World는 edge를 어떻게 정하는지에 따라 바뀔 수 있으므로 Navigable Small World의 구현체 및 검색 알고리즘에 대한 여러 논문들이 나와 있다(하단 Reference 7,8,9 참조). 이 글에서는 세부적인 구현 사항을 다루기보다 대략적인 검색/입력 원리만을 다루고자 한다.
NSW 검색
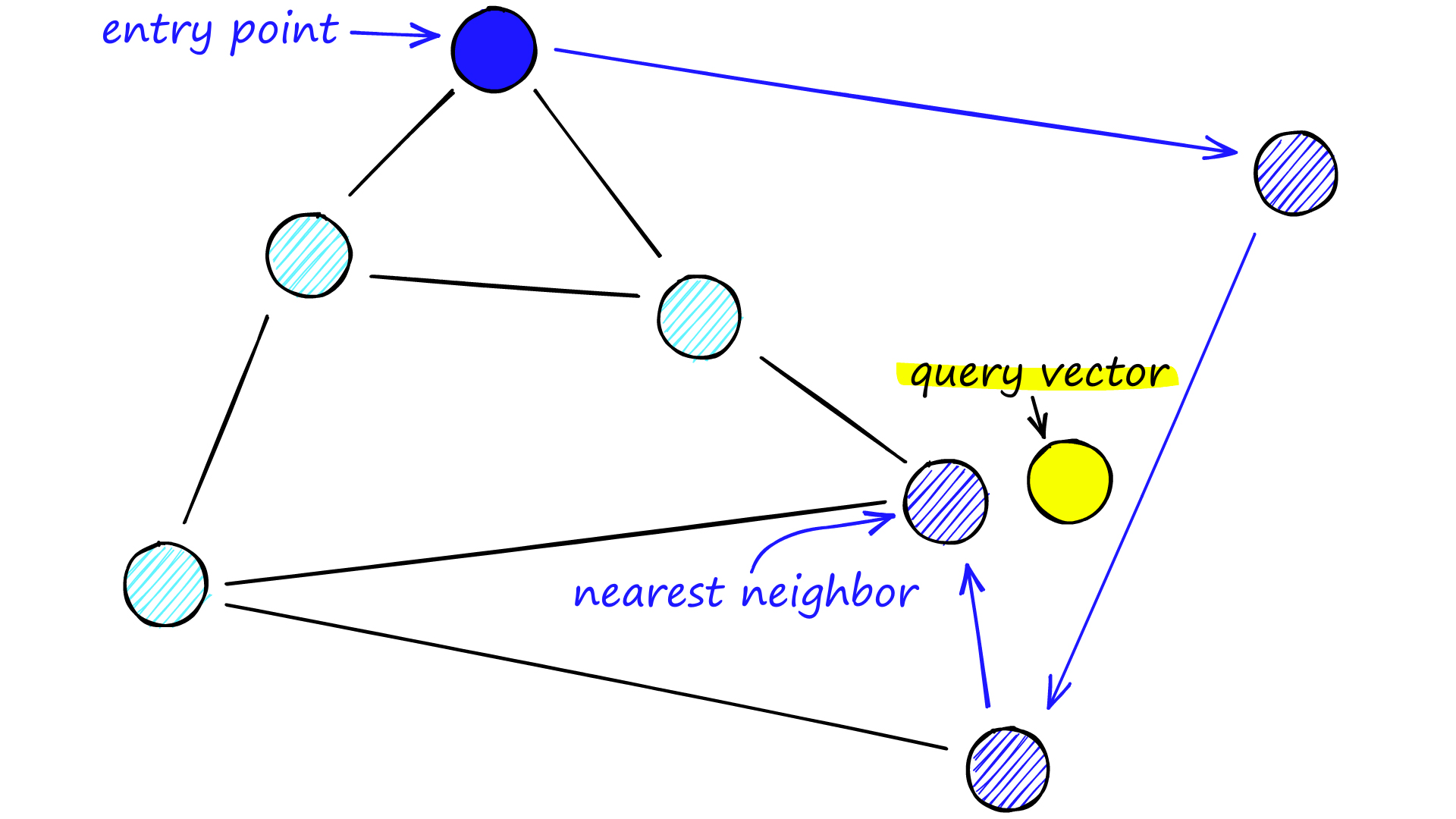
검색은 미리 정의된 포인트(entrypoint)에서 시작한다. 먼저 entrypoint와 연결된 정점을 쿼리 벡터와 비교하여 쿼리 벡터와 가까운 정점으로 이동한다. 이동한 정점에서 다시 연결된 정점들과 쿼리 벡터와 비교하고 이동하는 것을 반복한다. 즉, 각 스텝에서 쿼리 벡터와 가장 가까운 정점으로 이동하는 것이고 이를 greedy routing이라고 한다.
Greedy routing 결과로 나온 정점은 쿼리 벡터와 가장 가까운 정점이라고 보장할 수 없다. Greedy routing 검색 과정을 반복하면 어느 순간 현재 정점보다 쿼리 벡터에 더 가까운 정점을 찾을 수 없게되고 local minimum에 도착하게 된다. 하지만 이 local minimum은 쿼리 벡터와 어느 정도 가까울 수 있지만, 전체 데이터 셋에서 가장 가까운 정점은 아닐 수 있다.
심지어 local minimum에 일찍 도착하여 검색이 끝나버리면 꽤 부정확한 결과를 얻을 수도 있다. 이를 early stopping 문제라고 한다. 이를 해결하기 위해 여러 엔트리 포인트를 사용해 검색을 종합하면 정확도를 향상시킬 수 있다.
NSW 그래프 생성
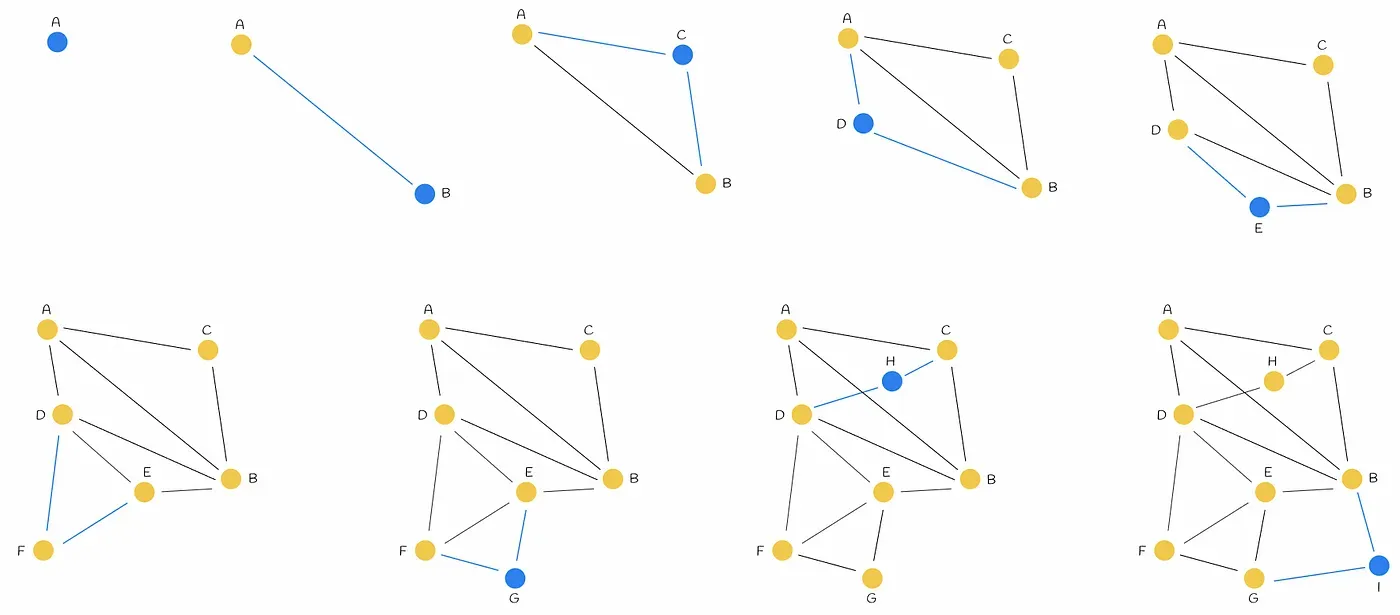
NSW 그래프는 데이터셋을 섞고 현재 그래프에 하나씩 넣으면서 만든다. 새로운 정점이 인입될때마다 M개의 가까운 정점과 연결한다.
NSW 그래프에서 긴 edge가 graph navigation에서 중요한 역할을 한다. 위 그림의 경우 AB가 초반에 추가됨으로써 긴 edge가 만들어졌는데, 이 edge가 그래프의 한 쪽에서 반대쪽으로 넘어가는 것을 쉽게 해준다. 만약 긴 edge가 없다면 정답과 먼 entrypoint가 잡혔을 때 부정확한 local minimum에 빠질 확률이 커진다. 이러한 긴 edge는 그래프 생성 초반에 만들어진다는 특징이 있다.
4. HNSW - Hierarchical Navigable Small World graphs
HNSW는 쉽게 말해 Skip list와 Navigable Small World의 핵심 아이디어를 합친 그래프 구조다.
HNSW는 2016년 논문으로 제안되었다. HNSW와 NSW의 복잡도를 비교하면 다음과 같다.
| HNSW | NSW | |
|---|---|---|
| Search Complexity | O(logN) | O((logN)^k) |
| Construction Complexity | O(N*logN) | O(N*logN) |
NSW의 Search Complexity가 polylogarithmic으로 표현되었지만 O(logN)에 가깝다. 즉, 복잡도를 보았을 때는 별 차이가 없다.
하지만 ANN 검색은 찾은 검색 결과가 실제 정답 검색 결과와 유사하게 나오는 것도 중요하다.
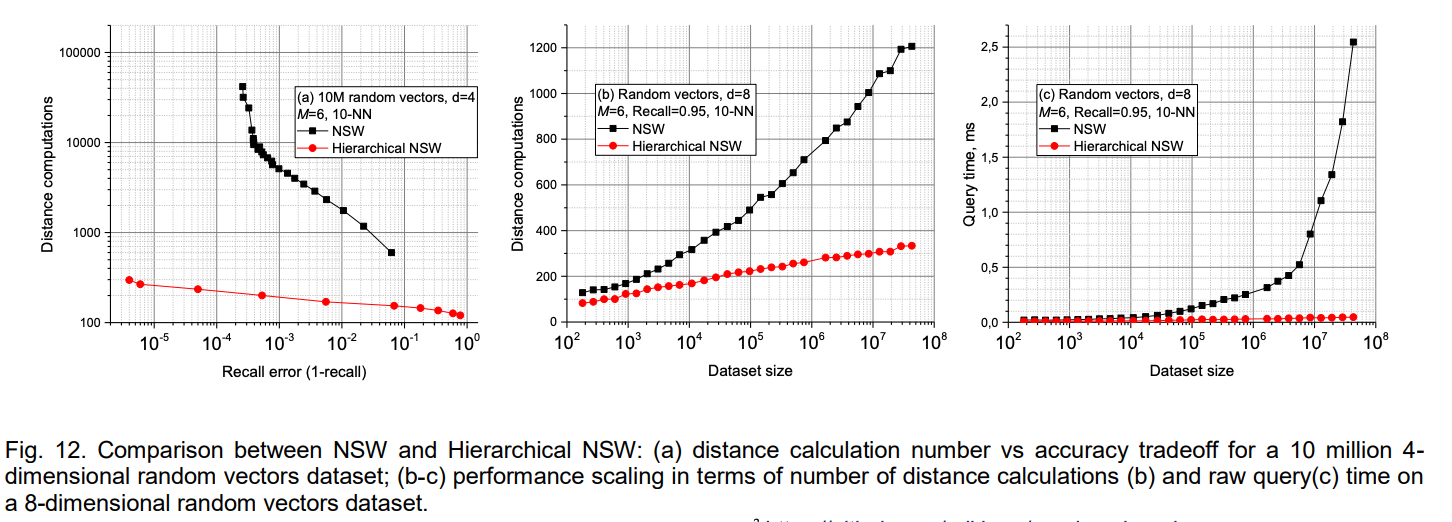
그래프 (a)를 보면 같은 정확도를 위해 HNSW가 계산하는 횟수가 NSW에 비해 현저히 적다. (b), (c)는 데이터 셋의 크기가 커질수록 HNSW의 성능이 NSW에 비해 좋은 것을 알 수 있다.
HNSW 검색
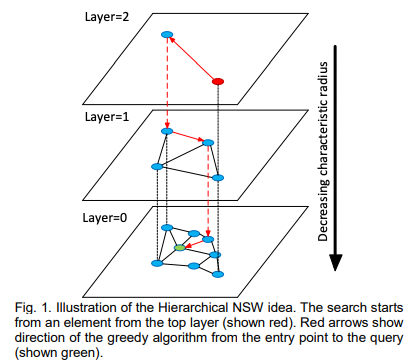
NSW의 단점은 정답과 먼 local minimum에 빠질 수 있는 것이다.
Entrypoint를 가장 차수가 큰 노드로 정해 검색을 시작하면 이를 어느정도 해소할 수 있다. 하지만 데이터셋이 커지면 커질수록 (1) 대부분의 greedy 검색이 동일한 노드를 통과할 확률이 높아지고 (2) 노드의 edge가 로그 스케일로 커지면서 검색 복잡도가 polylogarithmic에 가깝게 되는 단점이 있다.
HNSW의 핵심 아이디어는 NSW를 계층화해 edge를 길이에 따라 다른 계층으로 분류한다. 이를 통해 네트워크 크기에 어느정도 독립적으로 edge들을 평가할 수 있게되어 로그 스케일의 확장이 가능해진다.
HNSW의 검색은 가장 긴 edge를 가진 층인 최상위 계층에서 시작한다. NSW와 마찬가지로 각 계층에서 greedy하게 local minimum에 도달할 때까지 노드를 순회한다. local minimum에 도달하면 하위 계층으로 내려가고 이 과정을 반복한다. 모든 계층에서 노드당 최대 edge 개수를 제한하면 HNSW의 검색을 로그 스케일로 수행할 수 있다.
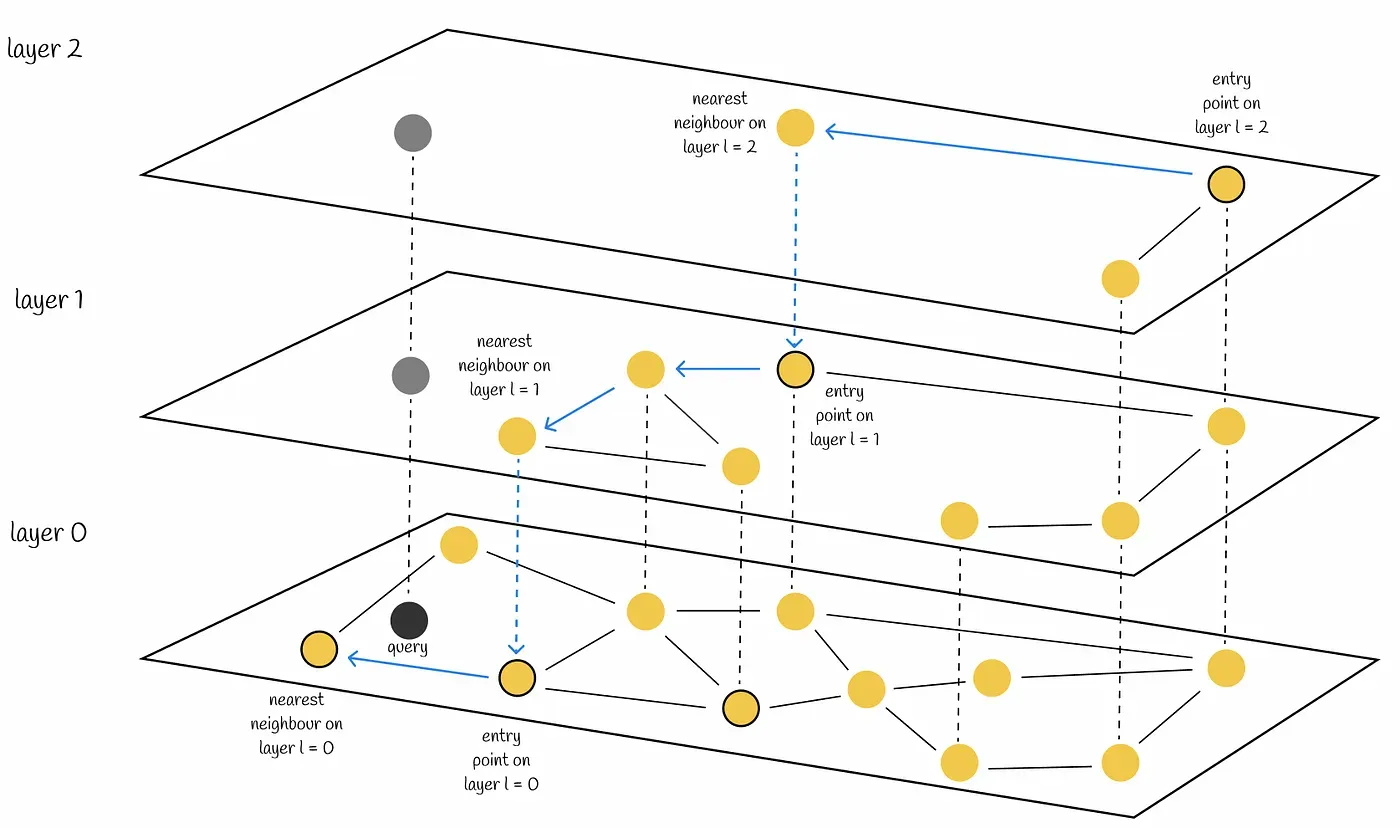
HNSW도 NSW처럼 여러 entrypoint를 사용하면 검색 정확도를 올릴 수 있다. 각 레이어에서 가장 가까운 이웃만 찾지 않고 여러 이웃을 찾아 다음 레이어의 entry point를 늘린다. 논문에서는 다음 레이어의 entrypoint의 개수를 하이퍼 파라미터로 조정한다.
HNSW 그래프 생성
HNSW 생성시 각 노드는 자신의 레이어 레벨을 할당받는다.
레이어 레벨은 ⌊-ln(unif(0..1))∙mL⌋로 계산된다. mL은 설정할 수 있는 파라미터로, 논문에서는 edge의 개수를 M이라고 했을 때 1/ln(M)을 최적 값으로 제안하고 있다. 레이어 레벨의 계산식에 로그가 씌워져 있어 상위 레벨로 올라갈 수록 노드의 개수는 기하급수적으로 감소하고, 대부분의 노드 레벨은 0이다.
노드가 레벨을 할당받으면 삽입은 두 phase로 이루어진다.
- 상위 레이어로부터 출발해 greedy하게 가까운 정점을 찾는다. 찾은 정점은 다음 레이어에서 엔트리 포인트로 활용된다. 할당 받은 레이어 레벨에 도착하면 두 번째 phase로 넘어간다.
- 정점을 현재 레이어에 넣는다. 이후 설정한 하이퍼 파라미터 개수만큼 가까운 이웃을 찾고 edge를 생성한다. 하위 레이어에서도 반복하여 레이어 0까지 삽입이 완료되면 알고리즘은 멈춘다.
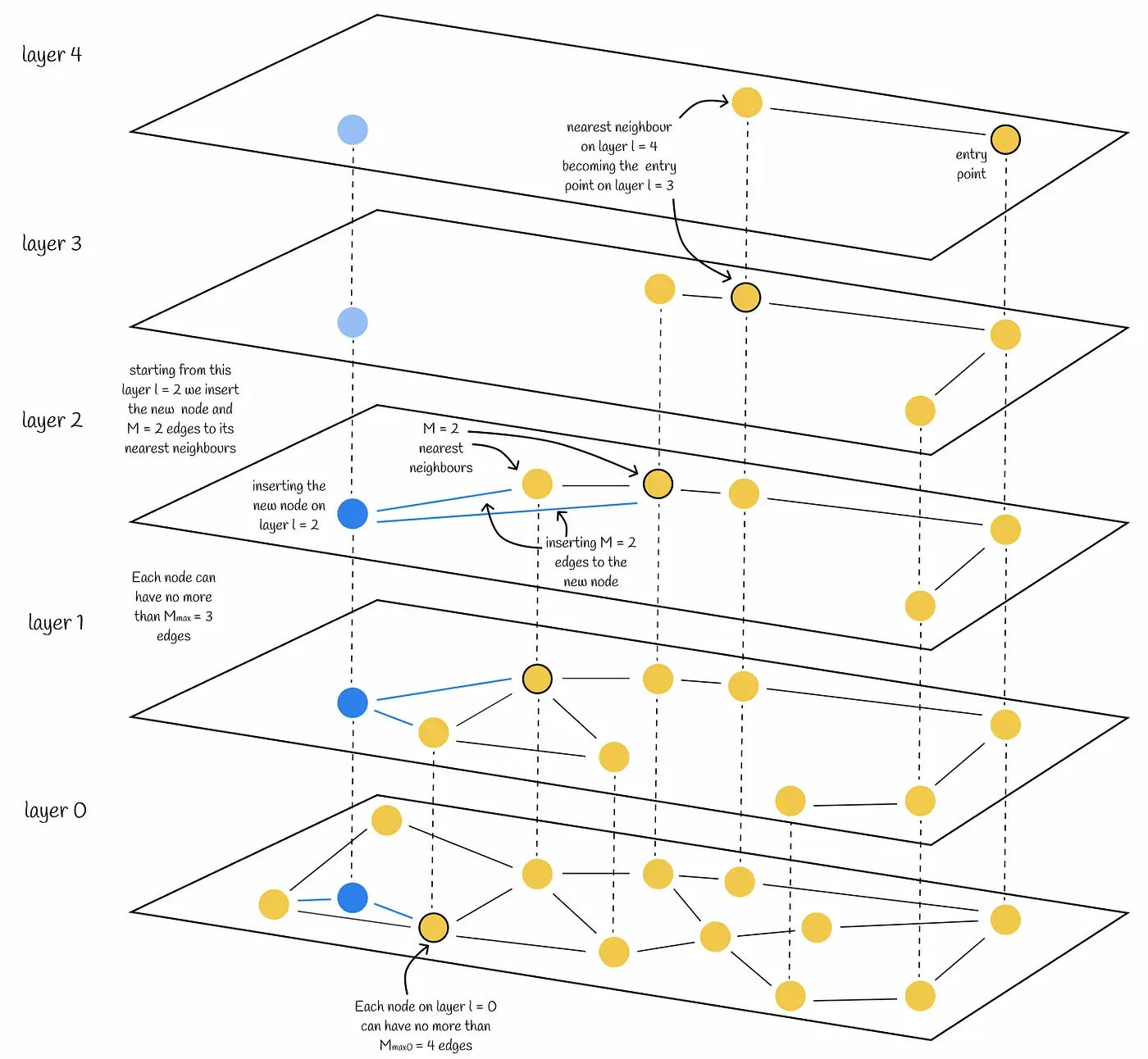
위 그림은 HNSW에서 레이어 레벨(l)=2, edge 개수(M)=2인 정점이 입력 후 연결되는 과정을 나타낸 것이다. 하위 레이어에 더 가까운 정점이 많아지므로 edge가 레이어마다 조금씩 달라지게 된다.
HNSW와 Skip list
HNSW의 계층화는 Skip list가 링크드 리스트들을 여러 레이어로 관리하는 것과 비슷하다. Skip list와 HNSW 모두 i번째 레이어에 등장하는 원소는 i+1번째 레이어에 확률 p로 등장하므로 상위 레이어로 갈수록 원소의 개수는 기하급수적으로 감소한다.
검색
상위 레이어에서 이동 범위를 크게 가져감으로써 이 두 자료구조는 데이터 셋의 크기가 커지더라도 비교적 좋은 검색 성능을 유지할 수 있다.
입력
대부분의 원소는 가장 하단의 레이어에만 입력되기 때문에 복잡도가 O(logN)으로 유지된다.
HNSW와 Inverted file index
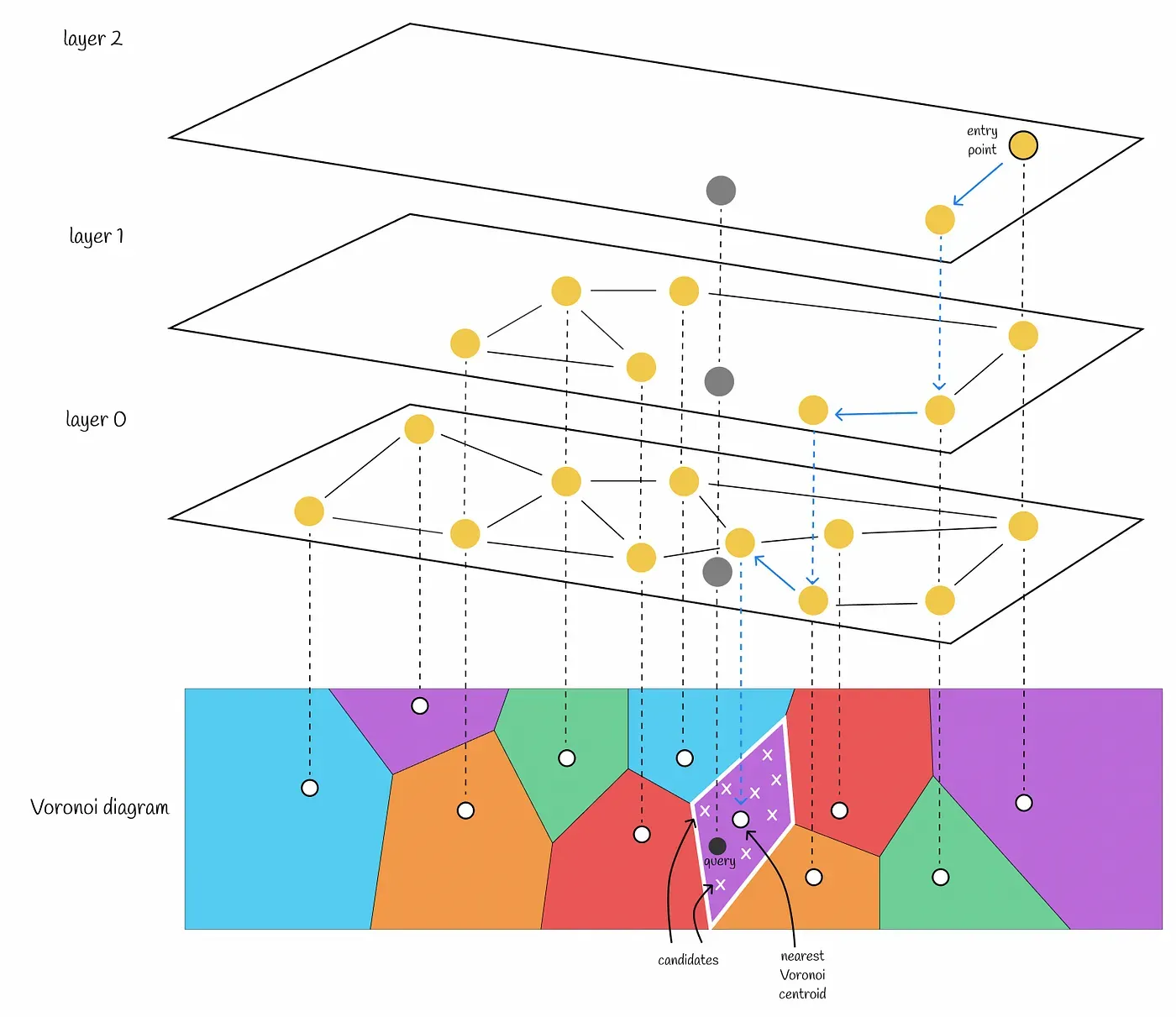
Voronoi diagram을 Inverted file index로 사용하면 유지할 수 있는 voronoi centroid 개수는 제한된다. Voronoi centroid가 많다면 cell을 선택하기 위한 brute force 검색시 시간이 너무 오래 걸리기 때문이다. 그래서 데이터 셋이 커지면 한 cell에 속하는 벡터의 수가 많아진다. 쿼리 벡터와 직접 거리를 계산할 후보 벡터 수가 늘어나는 것이다.
Voronoi diagram의 centroid들로 HNSW를 구축하면 이러한 문제는 사라진다. 즉 데이터가 많아져도 빠르게 가까운 voronoi centroid를 찾아낼 수 있기 때문에 한 cell에 속하는 벡터의 수를 적게하고 voronoi centroid의 수를 크게 가져갈 수 있다.
Reference
- Faiss.ai
- Skip List
- Pinecone-HNSW
- Similarity Search, Part 2: Product Quantization
- Similarity Search, Part 3: Blending Inverted File Index and Product Quantization
- Similarity Search, Part 4: Hierarchical Navigable Small World(HNSW)
- Y. Malkov et al., Approximate Nearest Neighbor Search Small World Approach (2011)
- Y. Malkov et al., Scalable Distributed Algorithm for Approximate Nearest Neighbor Search Problem in High Dimensional General Metric Spaces (2012)
- Y. Malkov et al., Approximate nearest neighbor algorithm based on navigable small world graphs (2014)

