When to stop using only bloom filters: Ribbon filter

This article is an english translation of the post that I published on the medium to share paper review
What kind of data structure should we use to determine which keys are in which sets?
The simplest way to do this is to use a hash map that holds all the keys, but the number of bits to store will become very large when the number of keys becomes very large.
Applications that need to store a very large number of keys, such as DBs, use bloom filters. Bloom filters can give a low probability false positive that a key exists even though it doesn't, but they can save a lot of storage space.
The Ribbon filter is a more space-efficient filter than the Bloom filter. RocksDB, which supports Ribbon filters, claims that Ribbon filters can save 27% of memory (for 100 million keys) at the cost of slightly more CPU than Bloom filters.
In this article, we'll take a quick look at some examples of using bloom filters and ribbon filters, and discuss the structure of ribbon filters.
Bloom filters on LSM trees
The LSM tree is one of the most commonly used data structures when implementing a DB.
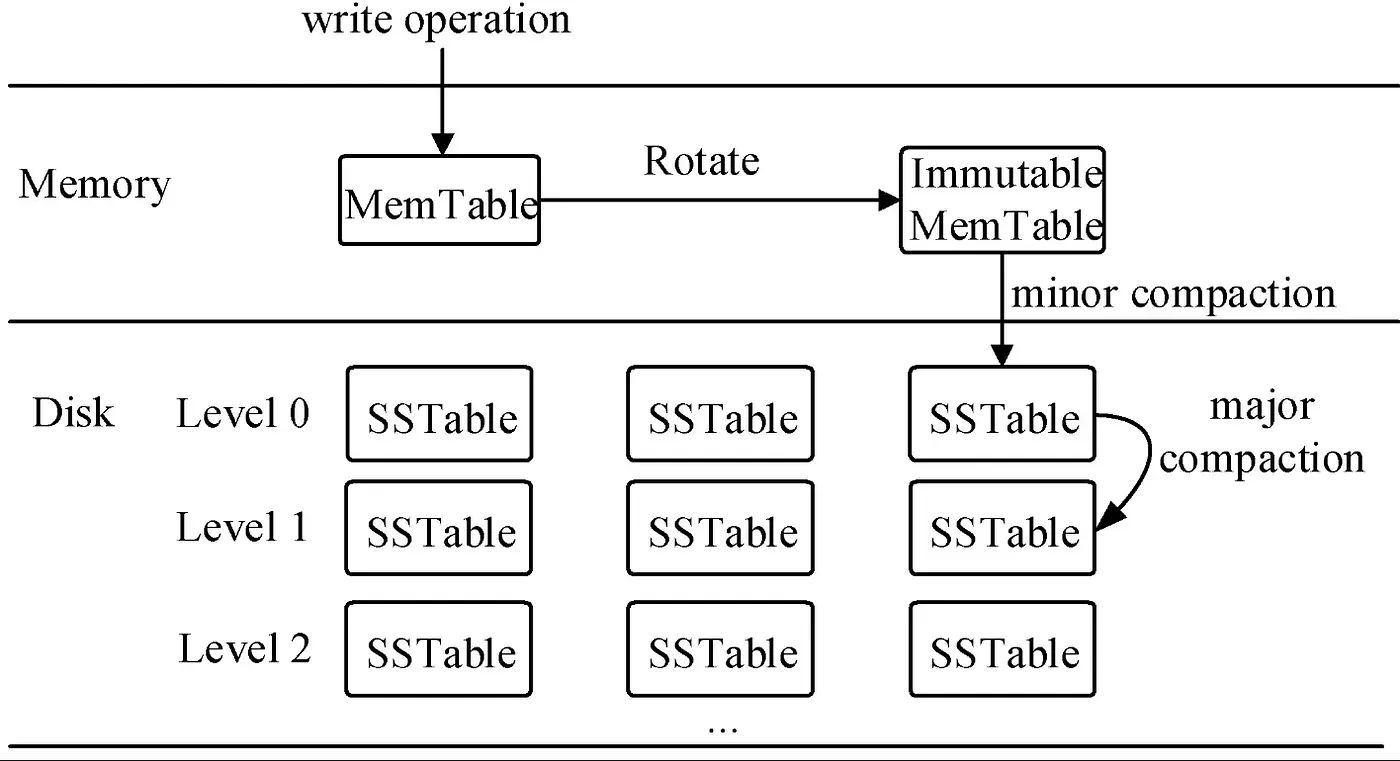
The LSM tree organizes SS tables into levels. In general, the larger the level, the larger the SS table and the older the data.
When a query comes from the LSM tree, it first checks the MemTable in memory to find the most recent data, and then works backwards from the lower level SSTables to the larger ones.
If it is looking for a key that doesn't exist in the DB, it can take a long time because it has to check all SS tables.
This is where the Bloom filter can be used to quickly return results, as it will know with a high probability that the key does not exist without checking all SStables.
Ribbon filters in RocksDB
RocksDB is a meta key value db library.
RocksDB uses LSM trees as its storage system, so the role of bloom filters is important.
According to RocksDB, bloom filters can consume more than 10% of RAM as the DB grows, so reducing the memory consumed by bloom filters is an important issue for users with large DBs.
There have been several probabilistic data structures like Bloom filters that tell you whether a key exists or not, but there hasn't been a good replacement.
- Xor filter, GOV: CPU usage 3-10 times greater than Bloom filter, while saving 15-30% space.
- Cuckoo filter: The amount of space saved varies greatly depending on the amount of false positives
However, the ribbon filter performed well as an alternative to the bloom filter. In RocksDB, using ribbon filters saved 27% memory for 100 million keys and 30% memory for 100 thousands keys compared to bloom filters with only modest CPU usage.
Given that CPU resources are typically more expensive than memory resources, bloom filters are favorable when the filter has a short lifetime and ribbon filters are favorable when the filter has a long lifetime.
RocksDB's simple math shows that if memory is alive for more than an hour, it is beneficial to use ribbon filters. On the other end of the spectrum, unless you have a write-heavy workload application that primarily uses short-lived memory, such as flash memory, you'll benefit from using ribbon filters.
Minimum number of bits a filter needs
Imagine you have a filter that has a false positive value of f. This filter must have at least log(1/f) bits per key, where log is the base of 2.
The very simple explanation is as follows:
Let S be the set of keys that the filter has, and U be the set of all keys.
The set T of keys for which the filter responds that they exist will then be the relation S ≤ T ≤ U.
When |S| = n, the space that the filter must cover is the space of subsets of size n in U. The filter must cover this space while satisfying a false positive f.
(1) The number of bits required by the filter is proportional to the number of keys, because the filter must unconditionally return that the key exists for all keys in S.
(2) In information theory, if an event has probability f, the information in that event is represented by log(1/f), where log base is 2. For example, if an event has a 25% probability of happening, we need at least 2 bits to represent that event.
By (2), log(1/f) is the minimum number of bits to have per key, and by (1), the filter must have at least n*log(1/f) bits when having a false positive f.
However, in practice, it is known that when f is larger than 2^(-4), filters use at least 20% more space than the theoretical lower bound.
Background: Filters and static functions
To understand Ribbon filters, you first need to understand static functions.
Static functions
Let S be the set of keys of a filter and U the set of all keys.
A static function is a function b(x) on S → {0,1}^r (where {0,1}^r is a space of dimension r that can only have 0,1).
The filter must return b(x) for any key x that belongs to S, but it will return any value in {0,1}^r for keys that do not belong to S.
Static functions and linear systems
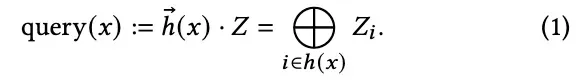
In the paper, they use h(x) and the row vector of h(x) (in equation (1) above, we label h(x) with vector). In this post, we will use h(x) as H(x) and the row vector of h(x) as h(x) in the paper)
The easiest way to create a Static function is to use multiple hash functions.
For |S| = n, prepare a set of hash functions satisfying h(x) ≤ [m] for any m ≥ n, where [m] is the set of natural numbers from 1 to m. The results of these h(x) correspond to {0,1}^m, respectively.
We often say that h(x) is a function that randomly picks 3 of the dimensions from {0,1}^m and sets them to 1.
For example, when m = 8, h(x) = {2, 5, 7} for some key x. The result of h(x) then corresponds to (0,1,0,0,1,0,1,0).
H(x) connects every key in U to some h(x).
Consider the set of h(x) associated with keys belonging to S. The result of a hash function h(x) matched with a key x has a result in {0,1}^m. If these results are linearly independent over {0,1}^m, then it is guaranteed that Z has a solution at h(x) * Z = b(x) for any x ∈ S. (Z ∈ {0,1}^(m*r)).
In other words, we can determine Z from h(x) and b(x) computed with keys belonging to S. Once Z is determined, computing h(x) * Z with keys belonging to S yields the same value as b(x) (The key exists). Computing h(x) * Z with keys that do not belong to S may or may not yield the same value as b(x). (False positives exist.)
As you might expect, as m and r get larger, the false positives will be smaller. The tradeoff for this is that the number of bits in Z, mr, will be larger, which will increase memory usage.
To summarize, for any key x belonging to U, a query on x has the following result
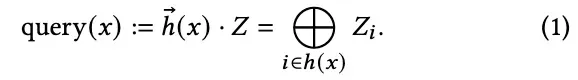
If this value is equal to b(x), it is returned as present; if it is different from b(x), it is not present.
The reason for the xor operation here is that the result of the dot operation is the same as xor when the elements of the dimension have only 0 and 1.
For example, if h(x) = {2,5,7} = (0,1,0,0,0,1,0,1,0), then the result of the query is equal to the result of a dot operation of h(x) and Z, which is equal to the result of an xor operation of their respective dimensions by subtracting the 2nd, 5th, and 7th rows of Z. The resulting value will have r dimensions since Z is {0,1}^(m*r).
Utilizing the above method, we can get a filter with 2^(-r) false positives by simply picking a function U → {0,1}^r at random and using it as a static function. This is because there is a 2^(-r) probability that the dot operation of h(x) and Z equals b(x).
An additional important point to note here is that the results of the static function must be linearly independent for the keys in S for a solution to exist, so we need to set m equal to or greater than n, the number of all keys, and if they are not linearly independent, the filter generation may fail.
Ribbon Filter
How does a ribbon filter get a static function? First, you need to know the SGUASS construction.
SGAUSS construction
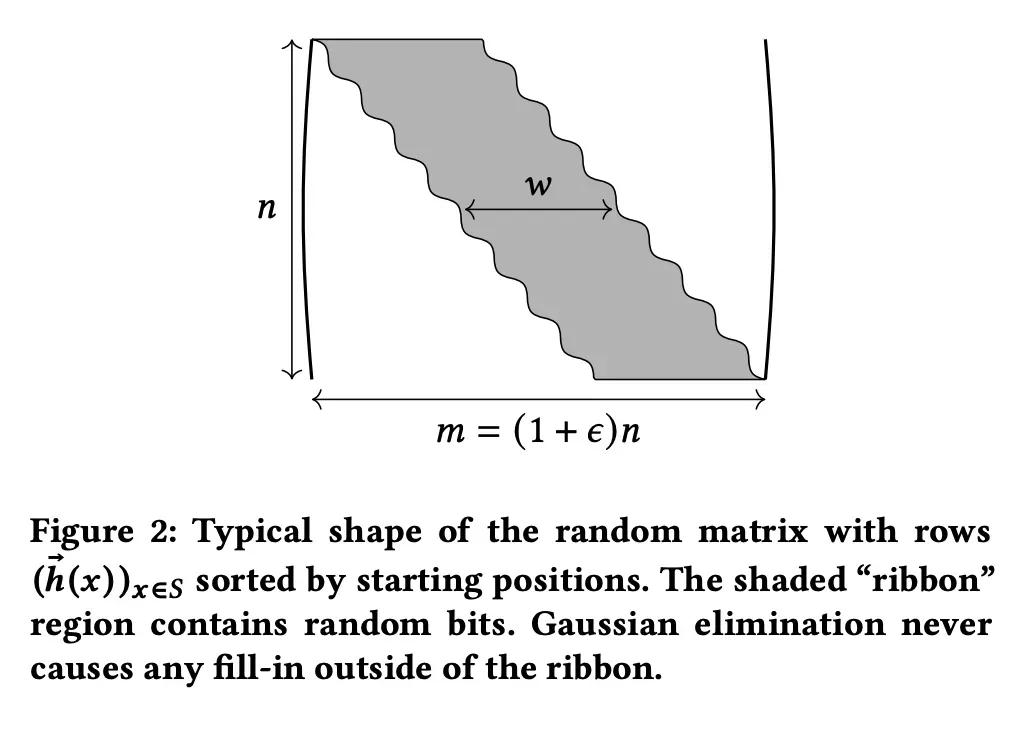
Figure 2 above shows h(x) sorted in order of where 1 starts. The colored part of the figure is called the ribbon, and only this region is filled with random bits, the rest with zeros.
Let's call the vector of colored parts in each row c(x) and say it has w bits ({0,1}^w)
Given a matrix of the form above, there is a proposition known as the following.
- The following proposition holds if 0<e<1/2, w = (logn)/e, and n/m = 1/e.
- For any static function b(x), there exists a solution Z such that h(x) * Z=b(x) with high probability.
- Once h(x) is sorted, Z can be solved in O(n/(e²)) by Gaussian elimination.
Note that for each row h(x) in H(x) in the figure, let s be the point where c(x) starts, h(x) can be represented by s-1 zeros, c(x), and (m-s-w+1) zeros. Then we only need to represent the index at which c(x) appears, so h(x) can be represented by log(m) + w bits.
Ribbon filters - on the fly
Ribbon filters use a similar method to SGAUSS. However, the process for creating filters is slightly different.
In the keystroke phase, we use a linear system M as shown below (we use an m * m matrix), and the first bit of c(x) corresponding to the ribbon must be unconditionally 1. We also use an on-the-fly Gaussian erasure method because we need to receive keystrokes in real time.
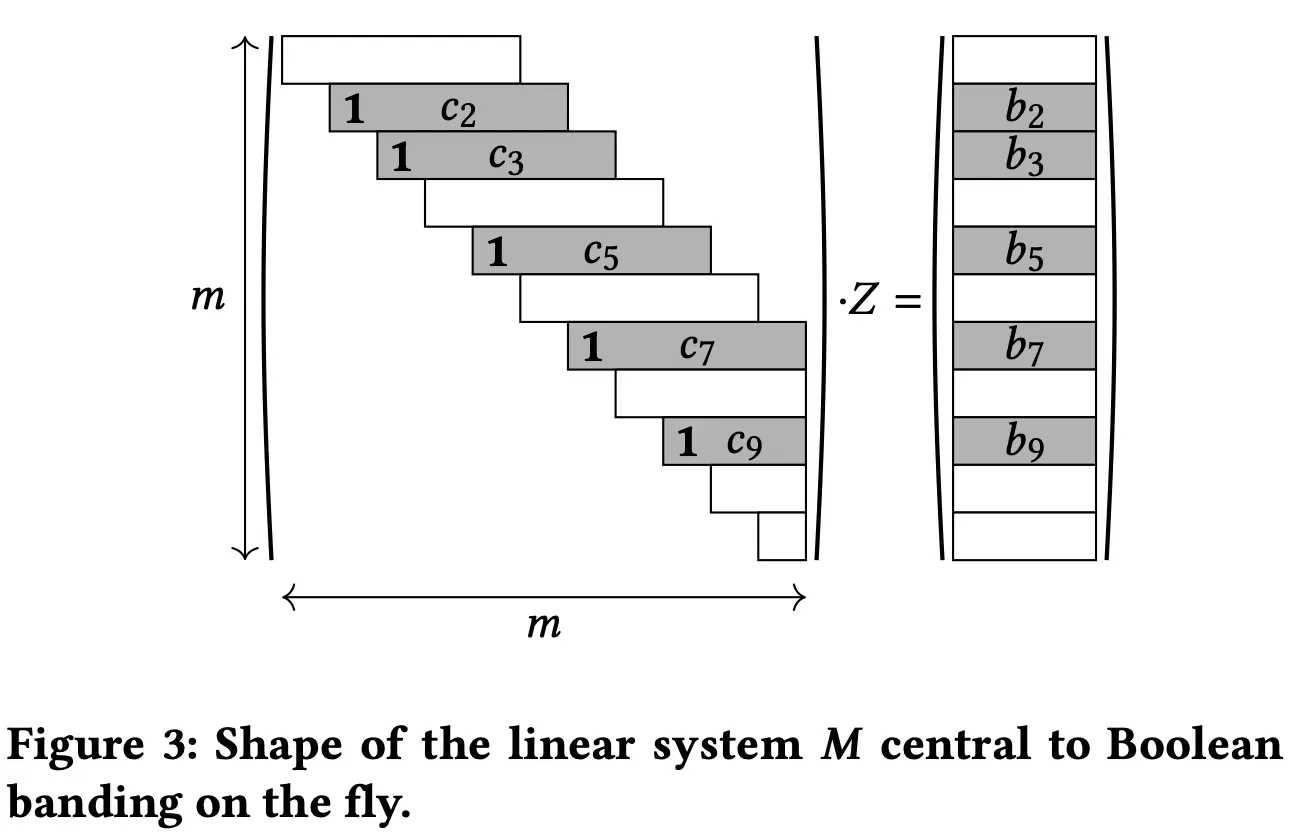
In the above figure, ci is {0,1}^w and bi is {0,1}^r. Since the parts except ci are zero, we only need ci and Z[i,i+w) to compute bi. (Z[i,i+w) is {0,1}^(w*r))
Assuming that h(x)*Z=b(x) is a one-to-one correspondence function for x ∈ S, we can use Algorithm 1 below in the input phase.

The goal is to reflect this in the linear system M when a key is entered (and return true when a query for that key comes in later)
Given a key x belonging to S, let i=s(x), c = c(x), and b=b(x).
Case1 - When the i-th row of M is empty
- If the i-th row of M is empty, use c and b in M as they are.
Case2 - When the i-th row of M is full
- Compute new c' and b' by XOR over the existing ci and bi.
- The c' and b' satisfy the following.
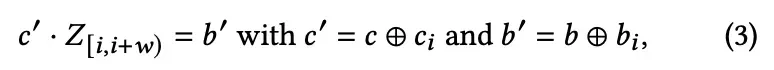
- By doing an xor, it is easy to determine if the rows being added are consistent with the existing linear system M
- If c' and b' are all zeros, it means that we already have the same key (0 when we XOR the same vectors).
- If c' is 0 but b' is not 0, the expression is unsolvable.
- If c' is not zero, count the number of zeros before the 1 in c'. Call this j, and repeat the loop by calculating i = i+j, c = c'>>j.
By entering the keys through the algorithm above, Z can be obtained from the bottom by Gaussian elimination. This is because the position where 1 starts, as shown in Figure 3, increases as the number of rows increases.
The above ribbon filter generation is characterized by an incremental key insertion, not a predetermined set of keys, but a real-time key can be added (on the fly), and not regenerated.
Nevertheless, the run-time difference between the SGAUSS method we looked at earlier and the ribbon filter generation is not proportional to the number of keys, but rather a constant difference.
The creation of SGAUSS and ribbon filters is essentially a solution to the same linear system. If the index calculated when the key came in already has M, the part that makes a difference is the part where the index is transferred and calculated. However, the algorithm always increases the recalculated index, which does not exceed m, so even assuming the worst-case scenario, it takes as long as the constant double difference.
Since it is known that SGAUSS can solve Z as O(n/(e²)), ribbon filters have the same O(n/(e²) complexity.
While looking at the paper, I was wondering how paper solved the situation where it was impossible to input because most of the M's were full when entering the key. Unfortunately, however, there was no mention of that part.
smash
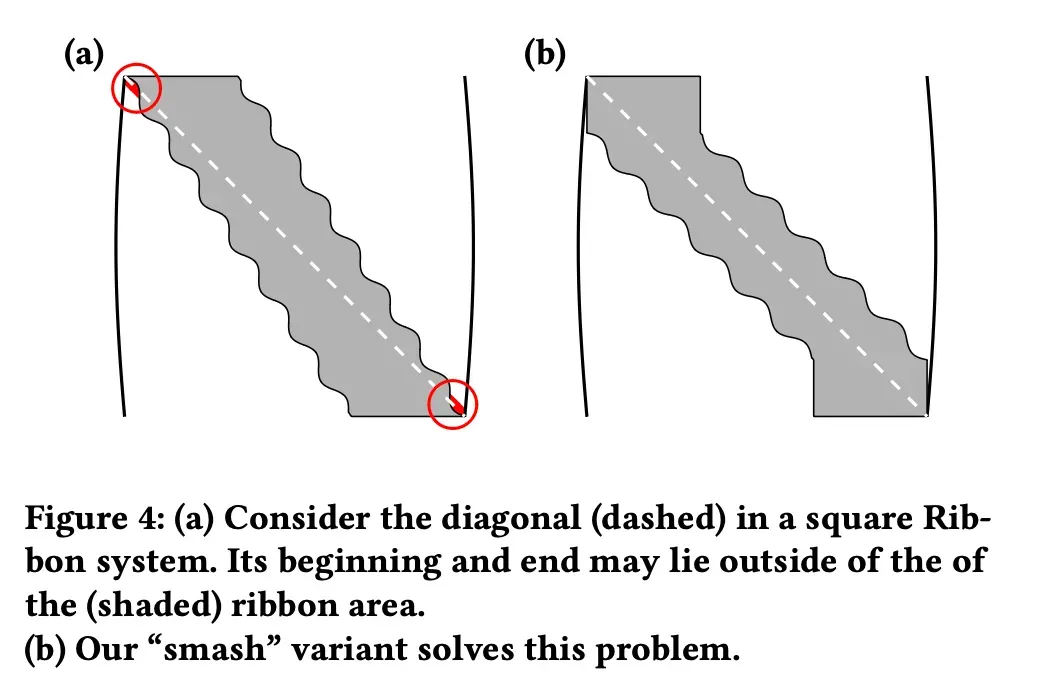
The role of each row becomes important as m gets closer to n to increase spatial efficiency.
If m=n, there is a very high probability that every row has a dimension of zero, then it cannot be solved. In this case, there are linearly dependent rows, and if the result (b(x)) is not a constant multiple, there is a case where there is no solution. However, if m=n, all dimensions have at least one row, there is no solution.
It is the first and last elements that have a high probability that all rows will be dimensions that can have zero. Therefore, as shown in Figure 4, we need to increase the probability that s(x) will be 1 and that it will be m-w+1. The parameter that adjusts the probability is called smash. Smash can create some overhead per query, but it increases the probability of containing diagonal lines as shown in Figure (b).
Optimizing Ribbon Filter
Configurability
Bloom filters allow you to use memory as efficiently as possible regardless of the number of keys, which is called configurability.
Unlike the Bloom filter, Cuckoo and Quotient filters use a fixed number of bits per cell to limit memory efficiency.
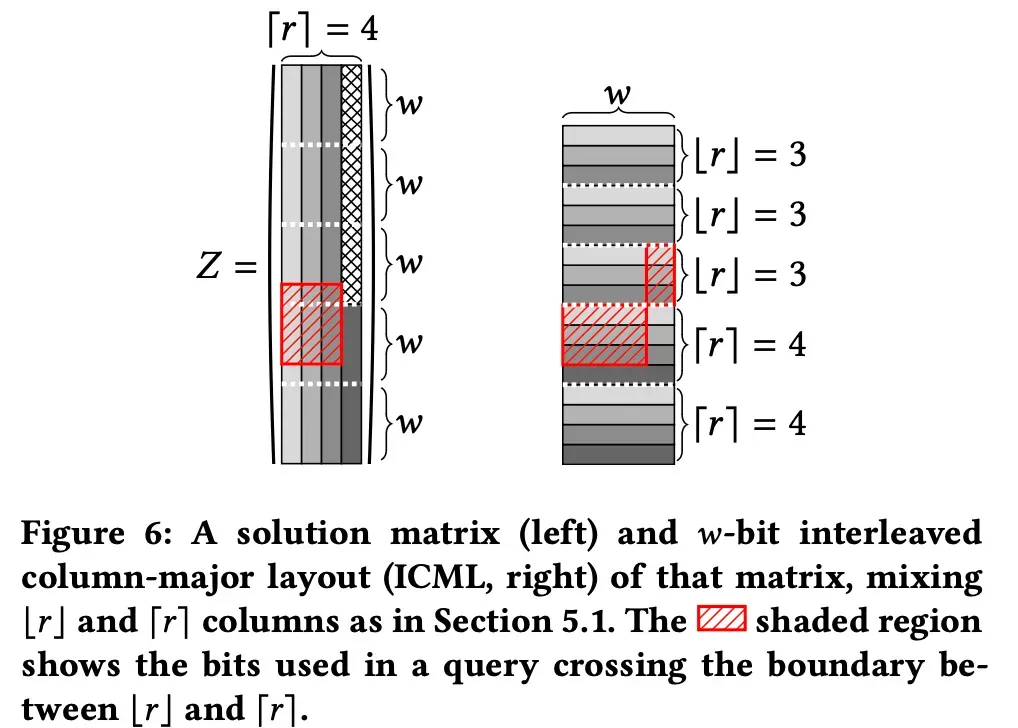
Instead of using r bits for every row, the ribbon filter uses a floor value of r for some and a ceiling value for others.
the appearance of a solution (Z) structure
There are usually two ways to store the calculated year (Z): row major and column major.
The column major method has the advantage of being able to handle the result value of the key in one memory access when r is 1. However, if r is greater than 2, the memory cache is inefficient and is not used well.
The ribbon filter uses Interleaved Column Major Layout (ICML). It stores each block in r words, and you can take advantage of the locality of the row major while still taking advantage of the column major's decoding.
Ribbon filter - Homogeneous Ribbon, Balanced Ribbon
Homogeneous Ribbon Filter
Among the ribbon filters, the static function b(x) set to 0 for all keys is called the Homogeneous ribbon filter.
- Pros: Success in filter generation is guaranteed, and scaling based on the number of keys is efficient
- Cons: False positive is higher than standard ribbon filter
A simple example of the disadvantage of a homogeneous ribbon filter is the case where all elements of Z are 0. In this case, the false positive is 1 and the condition of the solution is satisfied.
To prevent this, the Homogeneous filter randomly sets free variables (corresponding to rows empty in M) to prevent a true return for all queries.
Balanced Ribbon Filter
This filter optimizes scaling and spatial efficiency in standard ribbons.
The balanced ribbon introduced soft sharding in standard ribbons and a balance assignment scheme.
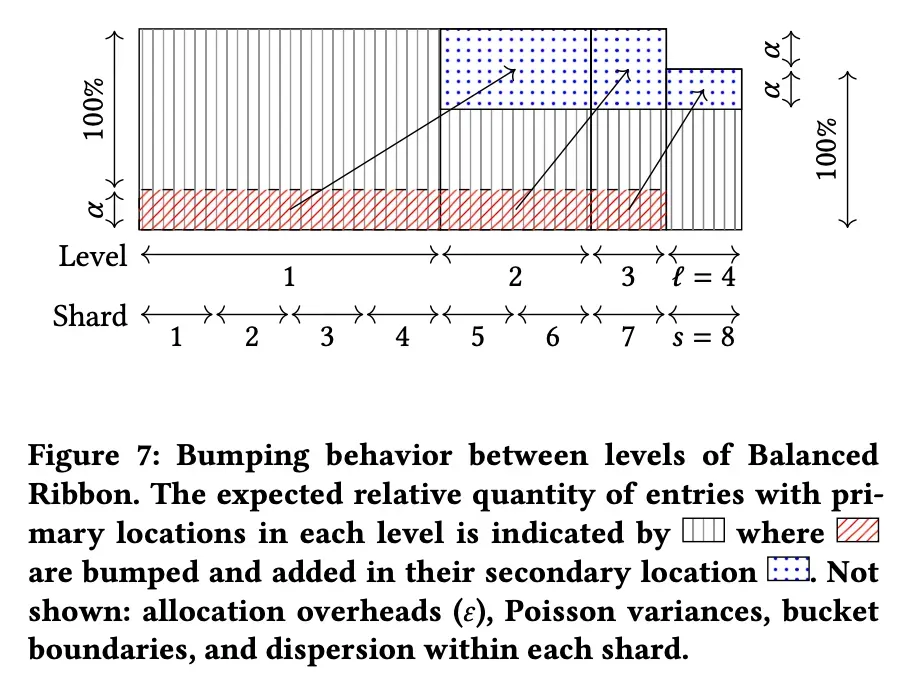
When a filter is created, each entry (key) can be stored in potentially two locations on the ribbon. Both locations are located in a separate shard determined by two hashes. The two locations are divided into primary and secondary and assign a key to the primary first. If the key already exists in the primary location, it is said to have been "bumped" and assigned to the secondary.
The balanced ribbon filter applied additional optimization factors such as dividing the shard into levels, please refer to the paper for more information.
Performance of Ribbon Filter
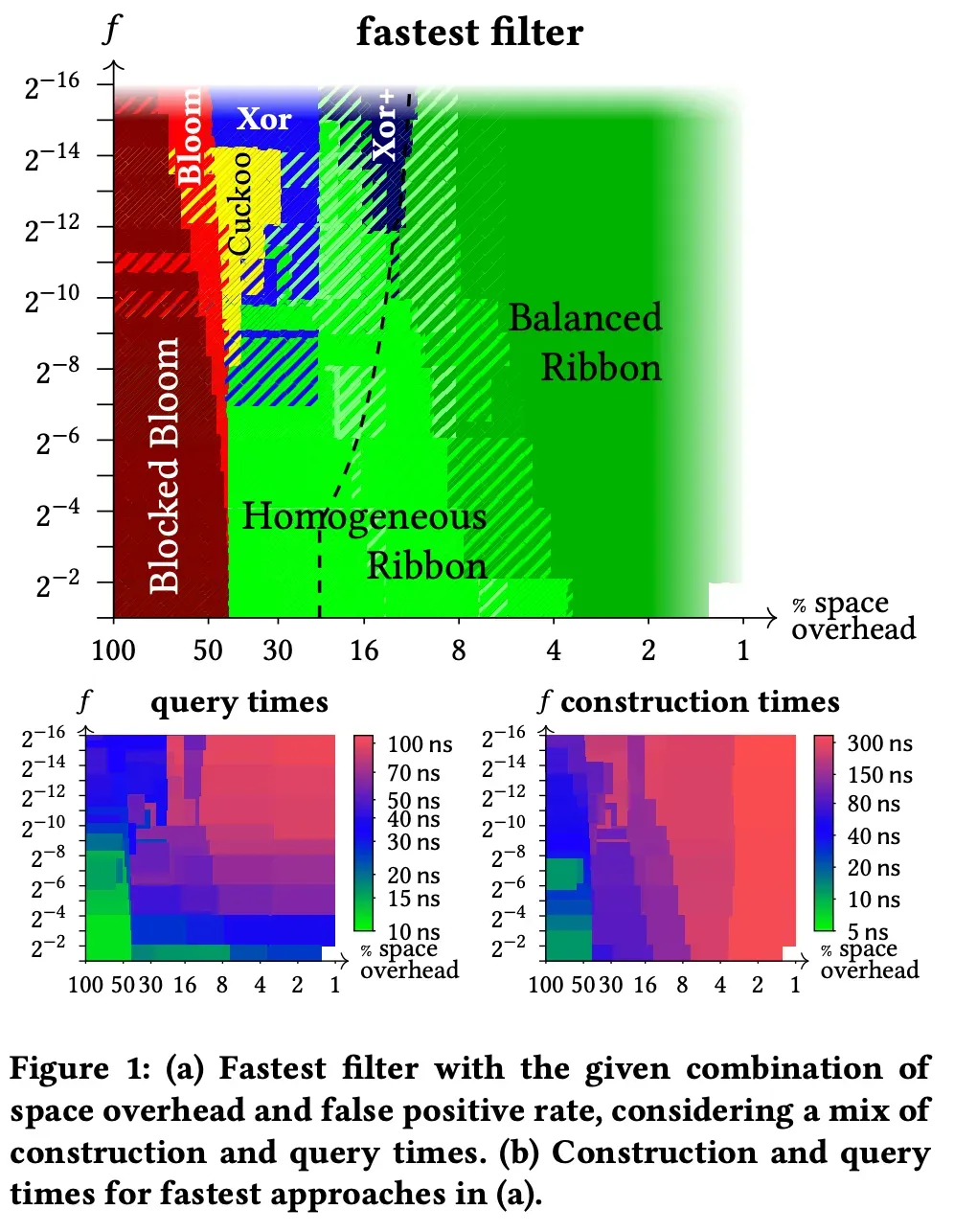
Figure 1(a) shows that Homogeneous and Balanced ribbons are the fastest filters at low spatial overhead.
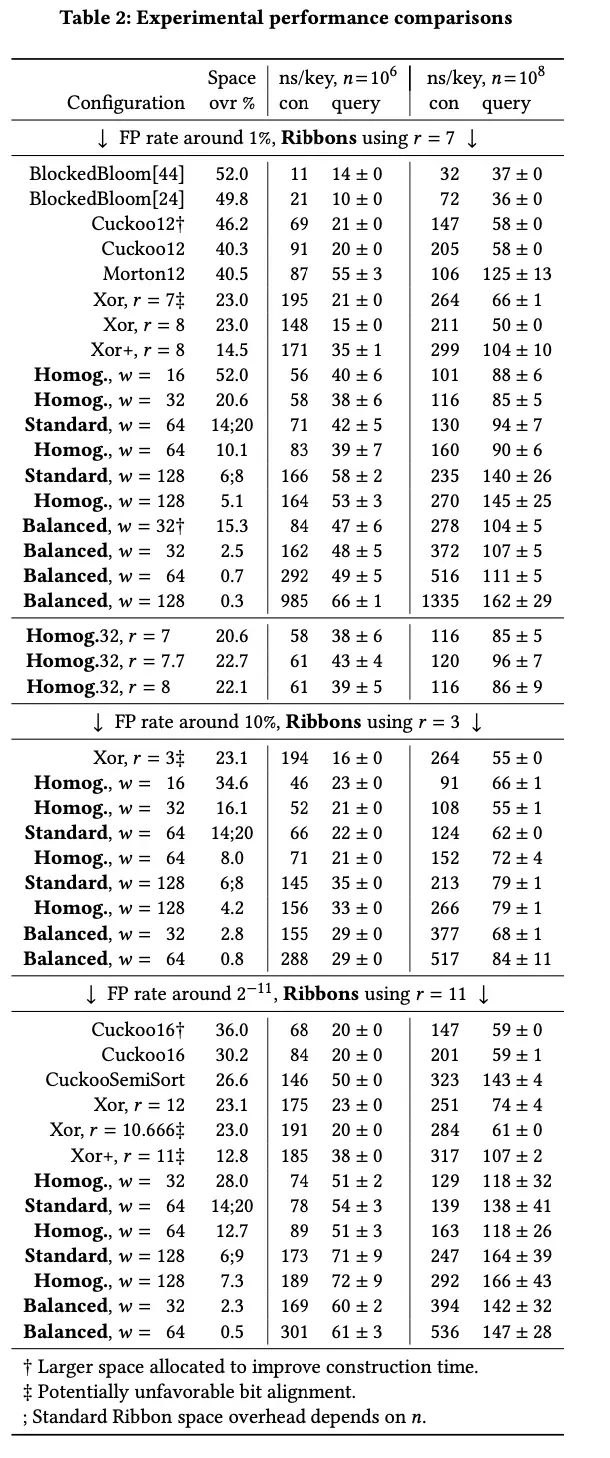
It can be seen that the ribbon filter has a significantly lower spatial overhead compared to other filters. At this time, it can be observed that there is a trade-off between spatial overhead and generation time.
The query time is typically the fastest for the xor filter, but if r and w are small, we can see that the query time for the ribbon is similarly fast.

