The paper we'll be discussing, Efficient Inverted Indexes for Approximate Retrieval over Learned Sparse Representations, was one of papers which won the Best Papers Award at SIGIR 2024.

This paper proposed an algorithm that performs vector searches in the inverted index solution often used in traditional search engines, rather than the graph based solution often used in vector search.

Introduction

Search is about fetching the documents that best fit a user's query.

Traditional search returns documents that contain many of the words in the user's query. A typical approach is to rank the documents with BM25 and fetch the top documents. However, this approach has the disadvantage of making it difficult to perform semantic search. For example, if a user enters "summer clothes" as a query, it is difficult to retrieve documents that contain the term "apparel for the warm season"

As language models have evolved to allow natural language to be embedded as vectors, it has become possible to use vectors to perform semantic-based search. There are two main types of vectors used in search. Dense vectors and sparse vectors.

Dense vectors are vectors with a relatively small number of dimensions. Documents and queries converted to dense vectors have nonzero values in most dimensions.

Sparse vectors, on the other hand, are vectors with a large number of dimensions. Typically, each dimension represents each token in the encoder model Vocabulary (ex: SPLADE). As a result, most of the dimensions are zero and the tokens in the query and document have non-zero values.

There are two major disadvantages when using Dense Vector.

1. Search results are hard to describe, which makes them difficult to tune and optimize, because it's hard for developers to know what each dimension of a Dense Vector means.
2. may not focus on the key words in a query and result in documents with similar meanings. Traditional methods such as BM25 weight rare words heavily, but Dense Vector methods can struggle because they convert queries/documents into vectors with meaning.

Due to these drawbacks, people usually use Sparse Vectors for search.

The advantage of Sparse Vector is that it is compatible with existing search engines that perform term-based search algorithms such as BM25.

Existing search engines manage <Term, Document id list with corresponding term>. If the search engine manages <Token, Vector id list with values in dimensions corresponding to the token>, it can be easily searched with a spare vector.

The "Effective Inverted Indexes for Approximate Retrievals over Learned Sparse Representations" we're going to talk about is that the structure of an existing search engine is compatible with the Sparse Vector, but it's not very efficient. And they propose a search engine structure that can serve the Sparse Vector well. If you're interested in search engine and vector search, it's going to be pretty interesting.

Before looking at the paper, we will first briefly discuss the concept of Sparse Vector search.

Sparse Vector Search

BM25 judges the importance of a term as tf-idf (term frequency - inverse document frequency). Simply put, the weight of a document for a term is higher with more terms in that document and fewer documents with that term.

The sparse vector is built by placing a simple neural network on top of a base model such as BERT, which makes the context vector. Because it is based on the context vector, the value of each dimension of the sparse vector represents the importance within the context. Unlike BM25, which indirectly predicts the importance of term, the importance is directly based on meaning.

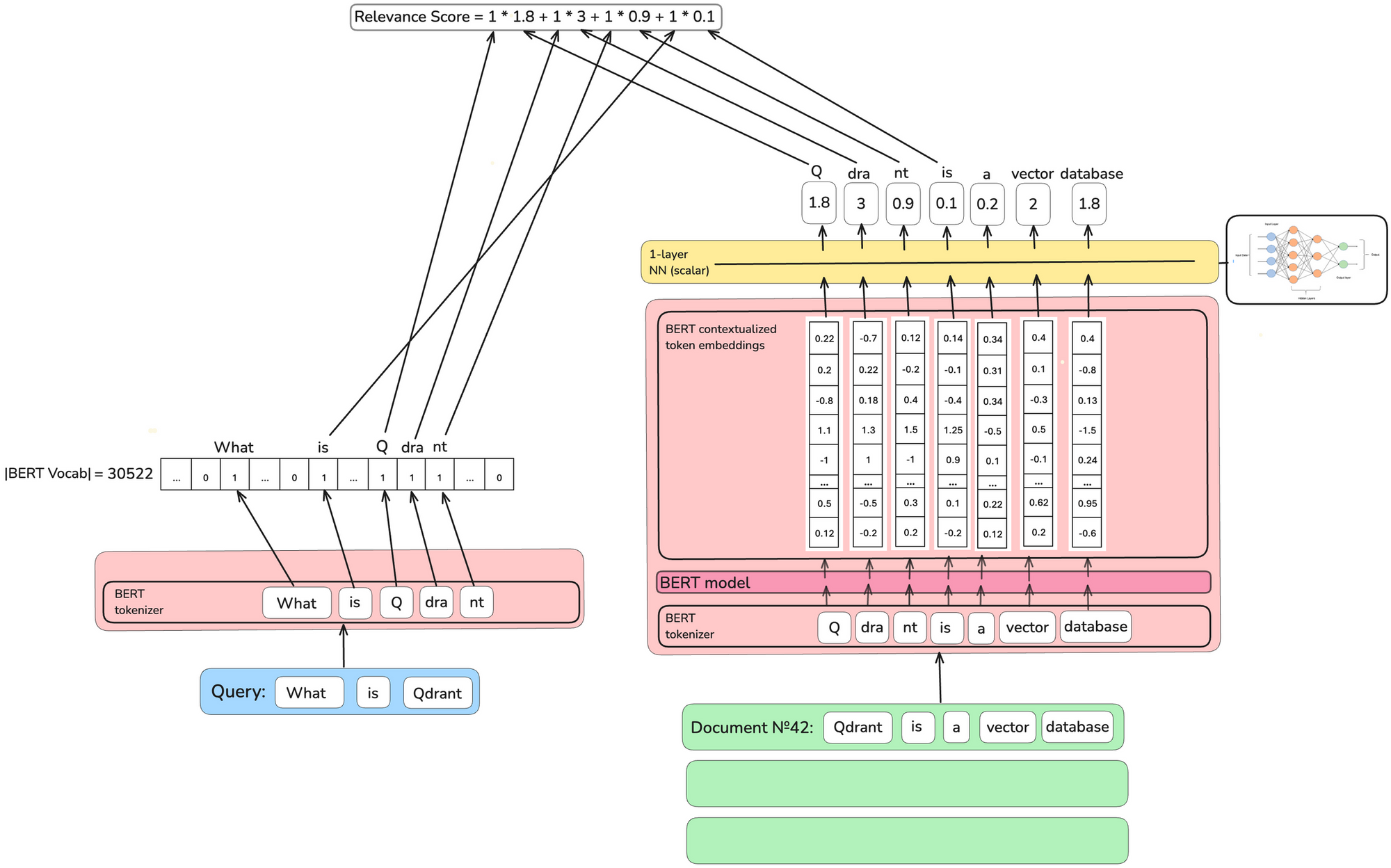
In the initial sparse vector model, TILDEv2, the document was tokenized and embedded, and weighted with one scalar value for each token.

It was a way of scoring the document by adding only the weight corresponding to the token generated by tokenizing the query.

However, there was a problem that the token had one scalar value, making it difficult to distinguish homonyms.

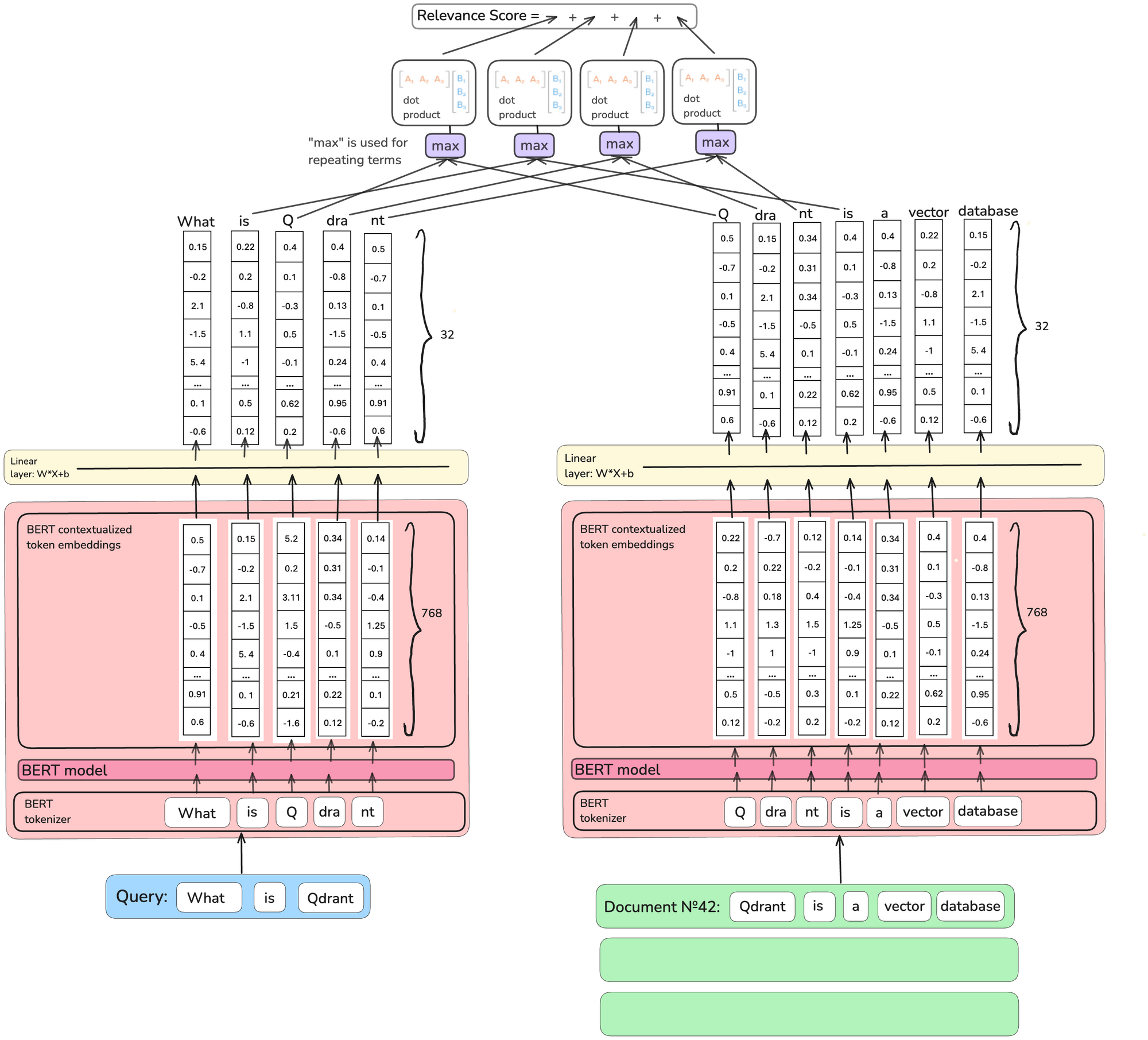
By taking the importance of the term into vector form(not scalar), we can solve this problem. Above, COIL model makes each token weight into a vector with 32 dimensions.

Because it internally multiplies the vector weights of queries and documents, if there is a token in the query and the document that is the same but has different meanings, the score will be low.

However, this approach was too expensive and did not fit well with the traditional inverted index search engine.

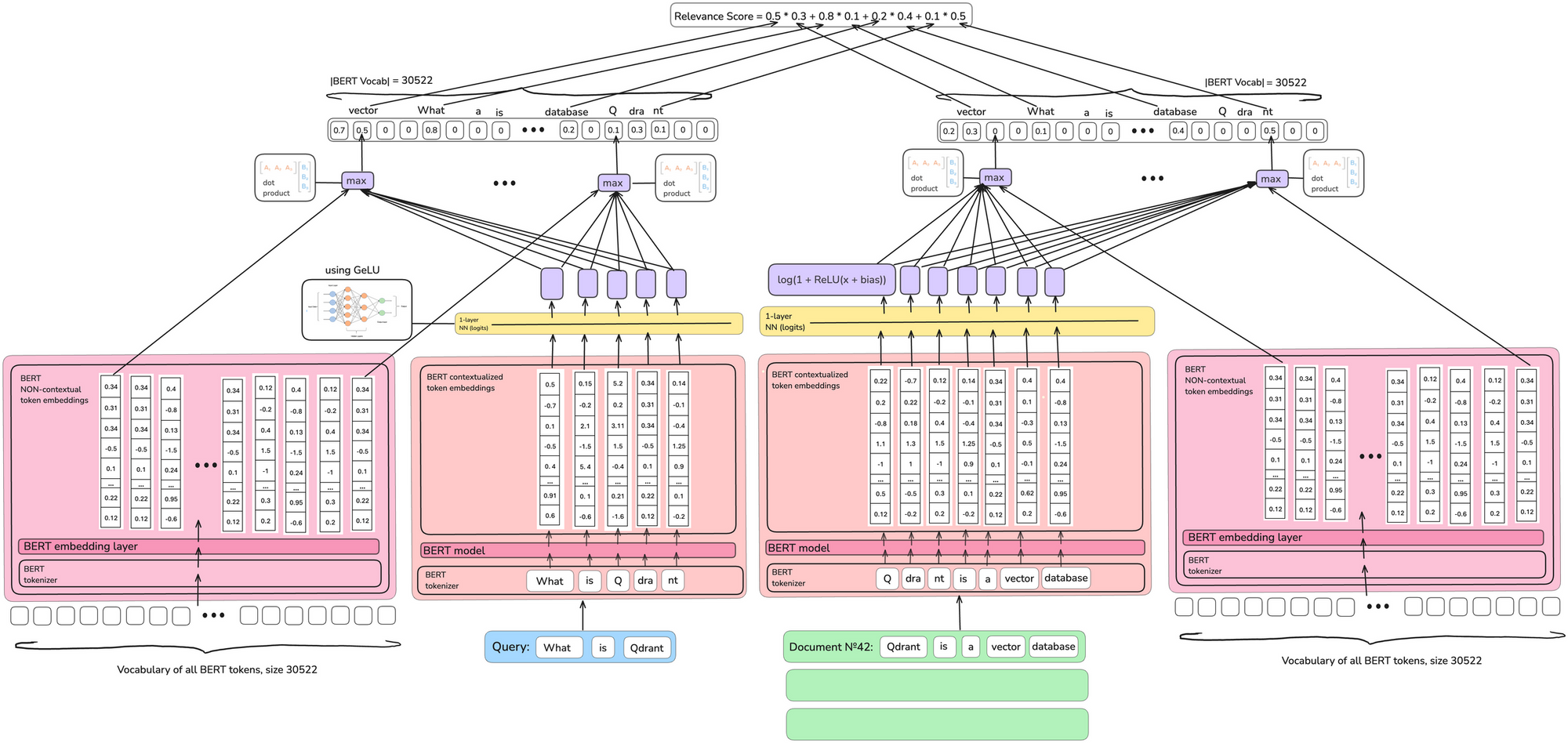
As of May 25, the most widely used model is SPLADE.

It is expensive to have vectors as weights for each token, so again the token has one scalar value.

However, for all token embeddings of BERT, dot product is performed to increase the number of non-zero tokens. This has the effect of expanding the document/query because tokens with similar meanings are added to the sparse vector.

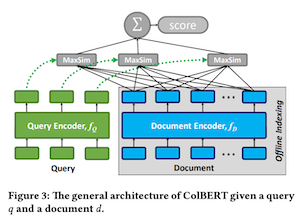
Do you remember ColBERT that we covered before? Compared to SPLADE, ColBERT is the opposite model.

• SPLADE makes one document a vector.
• ColBERT creates vectors in token units within a document, so one document is multi-vector.
• SPLADE is a sparse vector and each dimension corresponds to the weight of the term.
• ColBERT aims for fine-grained, token-level interactions between documents and queries.
• The vector of ColBERT is the dense vector.

Since ColBERT creates vectors in token units, it is relatively expensive compared to SPLADE, although less information is lost.

Because of the advantages and disadvantages of both methods, when creating a search service, take the model you use differently considering the characteristics of the service (and, of course, you may use other dense vector model).

Paper Reveiw: Efficient Inverted Indexes for Approximate Retrieval over Learned Sparse Representations

Now that we've looked into the Sparse vector model, let's look at the search engine structure proposed in this paper.

When serving SPLADE, you can easily serve by adding each dimension value of the spare vector instead of the weight to the search engine serving the inverted index algorithm such as BM25.

In this paper, the statistical nature of weights learned by Learned Sparse Retrievals (LSRs) is different from the assumption that inverted index algorithms operate, and the existing inverted index based search engines are inefficient when these search engines use LSR.

• Like WAND and MaxScore, term frequency model algorithms work well when queries are short and term frequency shows a Zipfian distribution.
• On the other hand, LSR has a long query length and, crucially, does not follow a Zipfian distribution, resulting in a longer response time per query

When deciding which documents to be included in a set of search results, WAND or MaxScore does not calculate all the scores on the document, but rather looks at the upper limit of the score a document can have and reduces the number of candidates for the score to be calculated. For this optimization to work well, the length of the inverted index's posting list must follow a Zipfian distribution. But the sparsity in the sparse vector is uniform for the dimension so it is ineffective.

The structure proposed by this paper contains a graph structure in inverted index. They decided that it would be better to use ANN in the sparse embedding serving. In fact, the paper was inspired by the fact that the graph-based ANN for the dense vector overtook the inverted index base algorithms in the 2023 NeurlPS Big ANN Challenge sparse embedding track.

α-mass subvector

One of the concepts you need to know before looking at this paper is α-mass subvector.

Define the vector normalization Lp as follows.

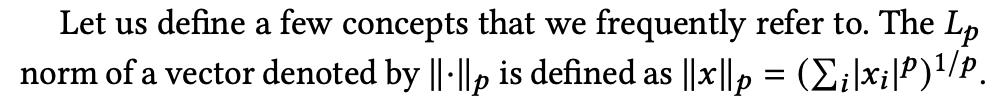
Use this normalization definition to define the α-mass subvector.

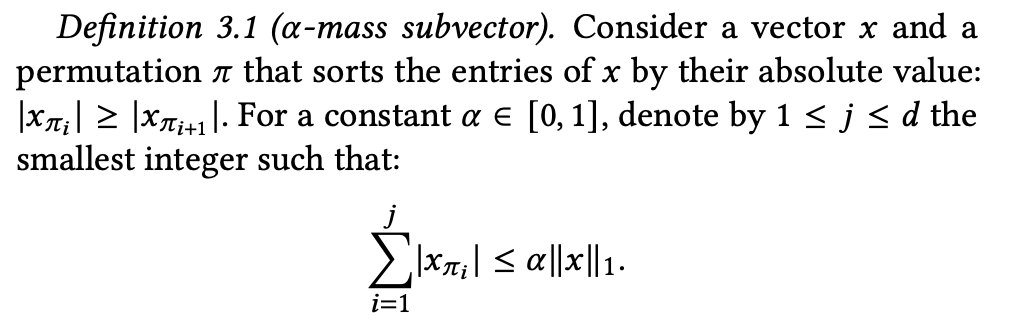
Simply put, if the value of each dimension of the vector is added in descending order and the value added from the first value to the jth is less than "the value added to the whole dimension (L1) * α", the vector that satisfies this is called α-mass subvector.

This concept is used to optimize the algorithm proposed by the paper.

Focus on what matters

Dimension values, which contribute a lot to the L2 normalization of vectors, also affect the dot product between vectors. Using this, we can reduce the collection size while almost maintaining the dot product value between vectors by discarding the value with probability proportional to L2 mass for dimensions with nonzero values.

In SPLADE and Efficient SPLADE, there is a logic that focuses only on important dimensions in proportion to the L1 mass of the vector. After embedding vectors with SPLADE in the paper, alpha-mass subvector was measured, and confirmed that top 10 entries in query made 0.75 mass subvector, and top 50 in document made 0.75 mass subvector.

The inner product between queries and vectors shows a similar phenomenon. In Figure 2, we calculated 85% of full inner product when we import top 10% of query and document's coordinates, respectively (Query 9, Document 20).

In summary, the LSR is concentrated in several coordinates, and the inner product between large entries can approximate the value of the entire inner product.

Proposed algorithm: SEISMIC

This paper proposes a SEISMIC algorithm that uses both an inverted and a forward index.

The Inverted index is used to determine the set of documents to be evaluated among documents.

The forward index is used to calculate the inner production of the document being evaluated.

(1) Inverted Index

The number of stored vectors: λ

As we saw earlier, the inner product's value can be approximated by calculating only a few important coordinates. SEISMIC takes advantage of this.

Let's call each element in the vector in order x1, x2, x3 … xn.

Create an inverted list of vectors x where xi is not zero for coordinate i. This inverted list is called li.

li is arranged in descending order with respect to the values of xi. At this point, we do not store all of the vectors, we store them up to λ. SEISMIC manages this λ as a hyperparameter.

In summary, λ serves as a parameter to control static pruning in the SEISMIC.

The number of blocks: β

The SEISMIC also has hyperparameters that control dynamic pruning.

Each inverted list is divided into β small blocks, where the β is the hyperparameter.

SEISMIC uses a clustering algorithm to divide documents in the inverted list into β clusters. The ids of documents in each cluster form a block.

In this paper, the clustering algorithm can be used regardless of supervised or unsupervised. The algorithm used in the experiment was shallow K-Means. It randomly selects β vectors from a set of vectors and use them as representative values of the cluster. And for all vectors, it calculates the similarity with these β vectors and assign them to the cluster with the largest value.

Number of vectors used to calculate the summary vector: α

SEISMIC performs dynamic pruning by looking at the block's summary vector when searching and deciding whether to evaluate documents in that block.

The summary vector is defined as the upper limit of inner product that can be obtained from documents in the block. The i-th coordinate of the summary vector is equal to the maximum xi of documents in the block. By calculating the inner product with summary vector, the search performance is improved by skipping documents in the block if the inner product does not exceed a certain level.

Note that the larger the block size, the larger the number of non-zero entries in the summary vector. It increases the space to store the summary vector and inner product computation time.

So when calculating the summary vector, it uses only the α mass subvector, where α is used as the third and last hyperparameter in SEISMIC.

In addition, the paper reduced the size of the summary vector by applying scalar quantization. By applying scalar quantization, only one byte can be used for each coordinate in the vector. Among the non-zero values in the vector, the minimum value, m, is subtracted from all non-zero coordinates and divided by subinterval. At this time, the subinterval must be set so that the maximum value is 255 and the minimum value is 0. When you recover the summary vector, you can multiply it again by subinterval and add m to recover it.

(2) Forward index

Forward index is an index to examine the exact document vector. It is used to calculate the documents and inner products in the query and block, and is performed only when the block is selected for evaluation.

Documents within the same block are not stored consecutively in the forward index, because the same document can be stored several times in different inverted lists, so there is a lot of cache miss in calculating inner product and it affects latency.

Summary of SEISMIC algorithm

Process of creating an Inverted Index

• Create d inverted lists for vectors in d dimension
• The inverted list has document id only and is sorted in descending order of coordinate value
• The inverted list stores only hyperparameters λ documents
• Each inverted list is clustered into β blocks
• Each block has a summary vector
• Use α mass subvector when calculating the summary vector

Query processing logic

• Extract important coordinates from query q (qcut)
• For each coordinate i of qcut, the block is evaluated using summary.
• If the summary estimate is higher than the minimum inner product of minheap, the documents in the block are evaluated
• When calculating inner product, use the forward index to get the complete vector of the document and calculate it.

Evaluation of SEISMIC

SEISMIC showed significantly better latency at the same accuracy compared to other algorithms.

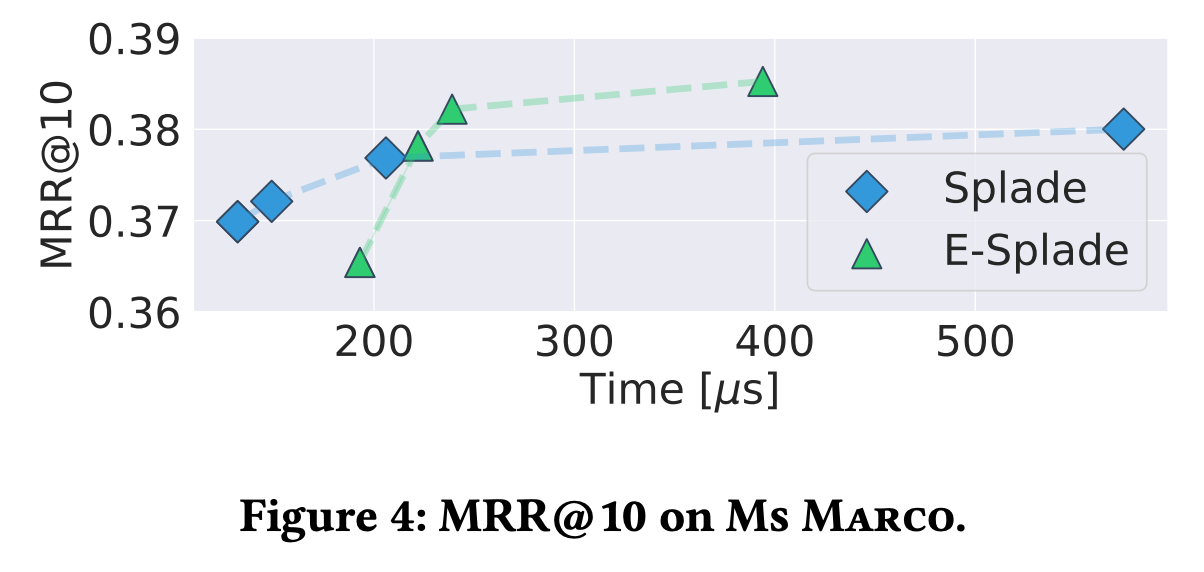
In the meantime, state-of-the-art inverted index solutions have used E-SPLADE, which can reduce query processing time because it is not fast enough when using SPLADE. With E-SPLADE, the search quality (NDCG, etc.) is poor compared to SPLADE in the zero-shot setting.

SEISMIC did not need to move to E-SPLADE because of the short query time even with SPLADE.

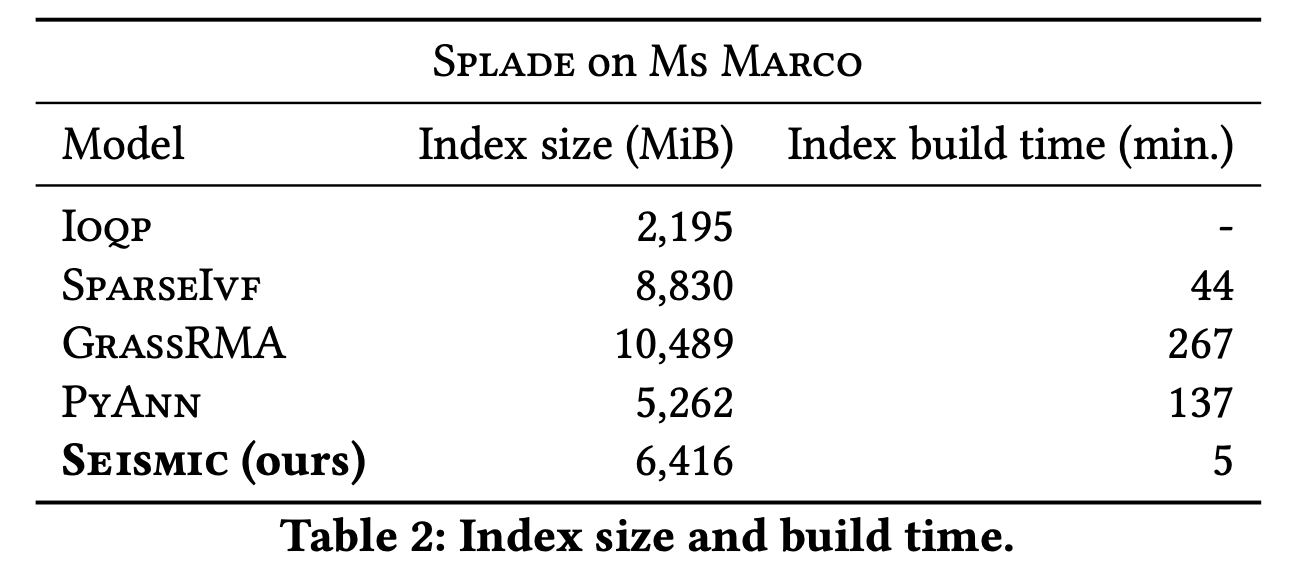
The size of SEISMIC's index is better compared to other algorithms and the build time is much shorter compared to other algorithms.

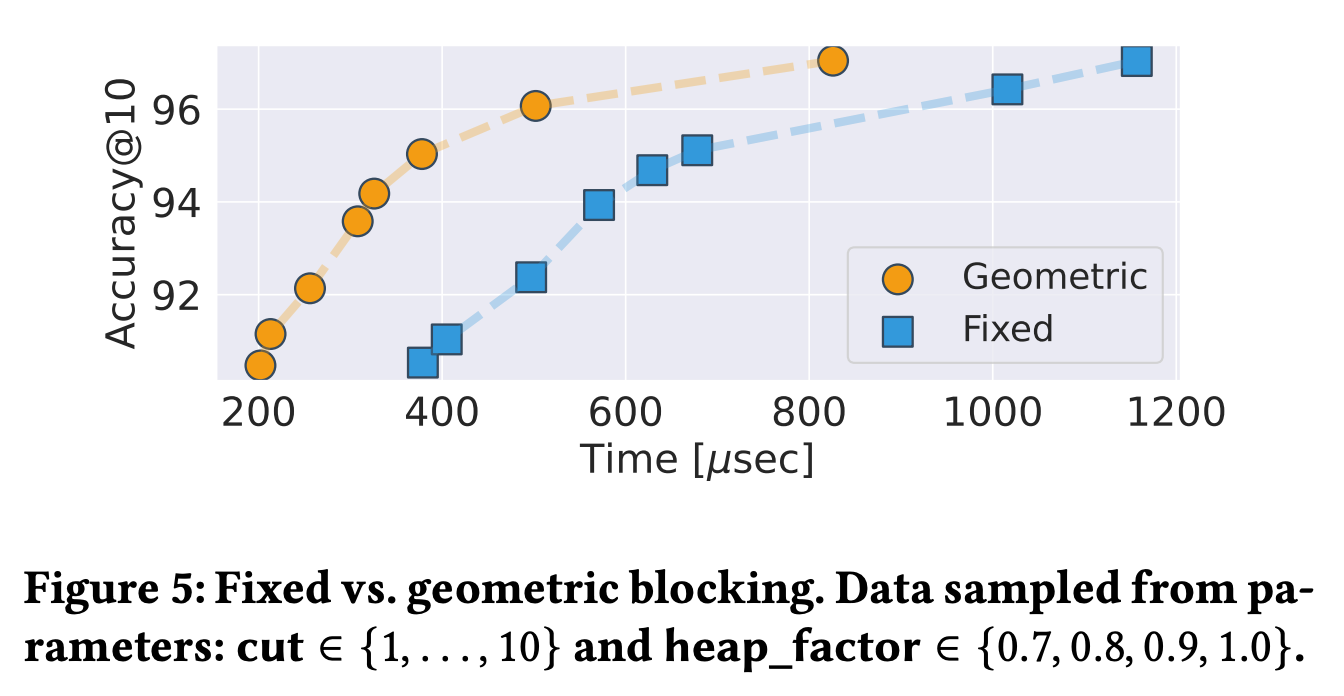
They show the performance difference between geometric (a K-Means-like approach) and fixed (a fixed-size chunk bundle) when splitting blocks. They find that using geometric blocking performs much better.

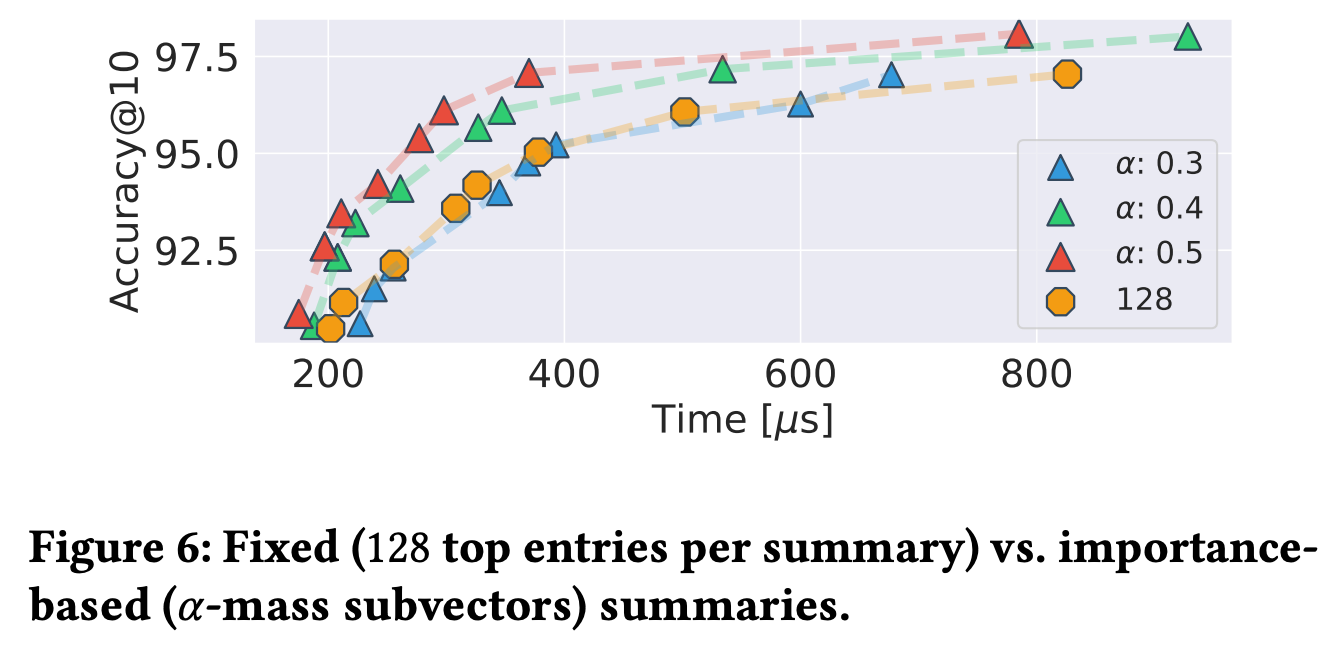
It shows the performance difference between calculating sumamr vector with a fixed number of entries and α mass subvector. The performance was much better when calculated with α mass subvector.

Wrap up

In this article, we looked at the reasons for using a sparse vector in search and SEISMIC, a new algorithm that serves the sparse vector in inverted index search engine structure.

It seems difficult to apply the SEISMIC to real-service search engines immediately for the following reasons. However, since these are sufficiently solvable problems, I think a search engine with SEISMIC can emerge.

• The search engine in service continues to receive vector input in real-time. Because SEISMIC fixes the number of blocks at β, blocks can continue to grow over time and become less efficient. If it becomes larger than a certain size, additional algorithms such as dividing blocks will be needed.
• If the search engine supports vector deletion/modification, an algorithm is needed to determine whether to modify the summary vector during vector deletion/modification.

Personally, it was interesting to optimize the value of inner product using α mass subvector, using the value of inner product being heavily influenced by a few important coordinates. It was also interesting to combine the clustering algorithm with the inverted index, which is the main idea of the paper.
From my perspective on creating a search engine, I think that idea is a useful one that can be used in the field.

Reference

Efficient Inverted Indexes for Approximate Retrieval over Learned Sparse Representations

Modern Sparse Neural Retrieval: From Theory to Practice