이번에 다룰 논문인 Efficient Inverted Indexes for Approximate Retrieval over Learned Sparse Representations 는 SIGIR 2024에서 Best Papers에 선정된 논문 중 하나입니다.

벡터 검색에서 자주 사용되는 그래프 방식이 아닌 기존 전통적인 검색 엔진에서 자주 사용되는 역색인 방식으로 벡터 검색을 하는 알고리즘을 제안합니다.

들어가며

검색은 사용자의 질의에 가장 적합한 문서들을 가져오는 것을 말합니다.

전통적인 검색은 사용자의 질의에 포함된 단어가 많이 포함된 문서들을 가져왔습니다. 대표적으로 BM25로 문서들을 랭킹하여 상위 문서들을 가져오는 방식이 있습니다. 하지만 이 방식은 의미 기반 검색을 하기 어려운 단점이 있었습니다. 예를 들어 사용자가 “여름 옷”을 질의로 입력했을 때 “하계 의류”가 포함된 문서는 검색되기 어렵습니다.

언어 모델이 발전하며 자연어를 벡터로 임베딩할 수 있게 되자 벡터를 사용해 의미 기반 검색을 할 수 있게 되었습니다. 검색에서 사용하는 벡터의 종류는 크게 두 가지로 나눌 수 있습니다. Dense Vector와 Sparse Vector입니다.

Dense Vector는 상대적으로 차원의 수가 적은 벡터입니다. Dense Vector로 변환된 문서와 쿼리는 대부분의 차원이 0이 아닌 값을 갖습니다.

Sparse Vector는 반대로 차원의 수가 큰 벡터입니다. 보통 각 차원이 인코더 모델 Vocabulary의 각 token을 의미합니다(ex: SPLADE). 그래서 대부분의 차원이 0이고 쿼리 및 문서에 포함된 토큰들이 0이 아닌 값을 갖습니다.

Dense Vector를 사용했을 때 단점은 크게 두 가지입니다.

1. 검색 결과를 설명하기 어려워 튜닝 및 최적화하기 어렵습니다. 개발자가 Dense Vector의 각 차원이 어떤 것을 의미하는 지 알기 어렵기 때문입니다.
2. 질의의 핵심 단어에 집중하지 못하고 비슷한 의미의 문서가 결과로 나올 수 있습니다. BM25와 같은 전통적인 방식은 희귀한 단어에 대해 가중치를 높게 주지만 Dense Vector 방식은 쿼리/문서를 의미를 가진 벡터로 변환하기 때문에 어려움을 겪을 수 있습니다.

이러한 단점으로 인하여 검색 작업에 이용하는 벡터는 보통 Sparse Vector들을 사용합니다.

Sparse Vector는 BM25와 같은 term 기반 검색 알고리즘을 수행하는 기존 검색 엔진과 호환이 잘 된다는 장점이 있습니다.

기존 검색엔진은 <텀, 해당 텀을 가지고 있는 문서 id 리스트>를 관리합니다. 검색엔진이 <토큰, 해당 토큰에 대응되는 차원에 값을 가지고 있는 벡터 id 리스트>를 관리하면 쉽게 sparse vector로 검색을 할 수 있습니다.

이번에 다룰  “Efficient Inverted Indexes for Approximate Retrieval over Learned Sparse Representations” 은 기존 검색 엔진의 구조가 Sparse Vector와 호환되지만 효율이 좋지 않았다고 말합니다. 그리고 Sparse Vector를 잘 서빙할 수 있는 검색 엔진 구조를 제시합니다. 검색 엔진 및 벡터 검색에 관심이 있으신 분들은 꽤 흥미로운 내용이 될 것입니다.

논문을 살펴보기 전 먼저 Sparse Vector 검색의 개념을 간단히 다루겠습니다.

Sparse Vector 검색

BM25는 term의 중요도를 tf-idf (term frequency - inverse document frequency)로 판단합니다. 간단히 말하면 어떤 term에 대한 문서의 가중치는 term이 해당 문서에 많이 나올수록, 그 term이 나온 문서가 적을 수록 높아집니다.

Sparse Vector는 context vector를 만드는 BERT와 같은 베이스 모델 위에 간단한 뉴럴 네트워크를 얹어 만듭니다. Context vector를 기반으로 하기에 sparse vector의 각 차원의 값은 context 내 중요도를 나타냅니다. 간접적으로 term의 중요도를 예측하는 BM25와 달리 의미를 기반으로 중요도를 직접 매기게 된 것이죠.

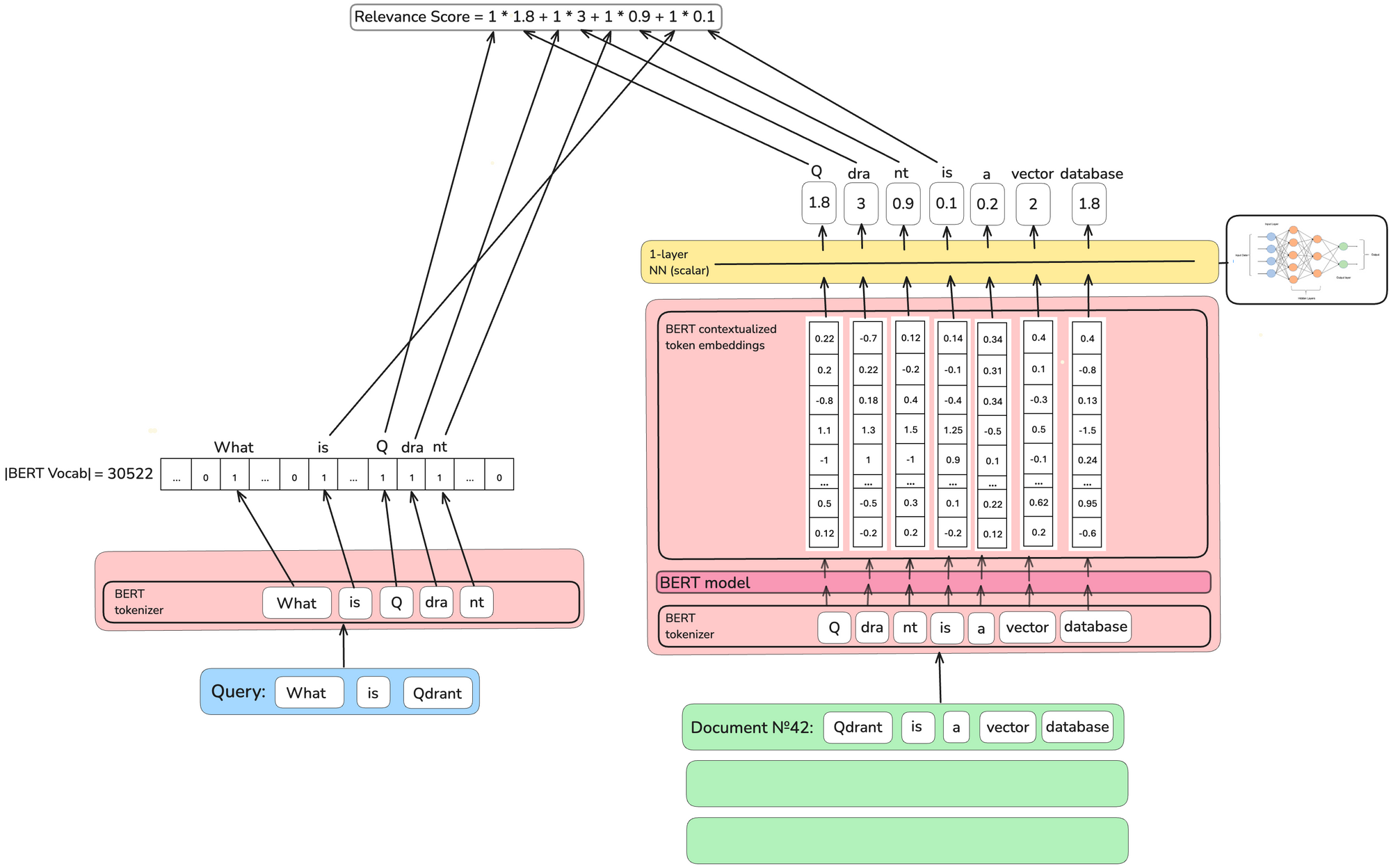
초기 sparse vector 모델인 TILDEv2에서는 문서를 tokenize하고 임베딩한 뒤 토큰마다 하나의 스칼라 값으로 가중치를 계산하였습니다.

쿼리를 tokenize하여 생성된 토큰에 해당하는 가중치만 더하여 문서의 점수를 매기는 방식이었죠.

하지만 토큰이 하나의 스칼라 값을 가져 동음이의어를 구별하기 힘들다는 문제가 있었습니다.

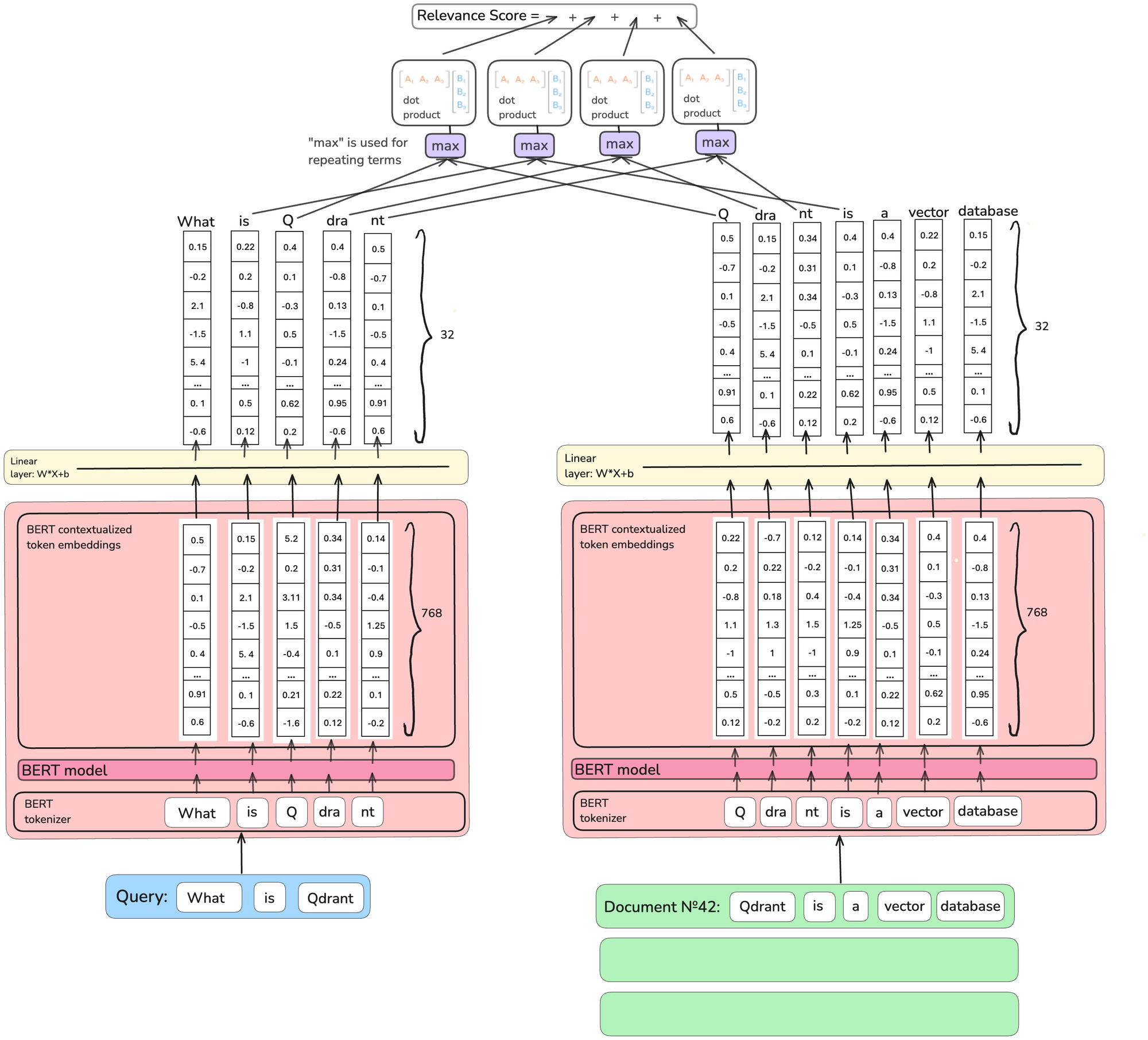
텀의 중요도를 벡터 형태로 만들면 이를 해결할 수 있습니다. 위는 COIL 모델로 각각의 토큰 가중치를 32개의 차원을 가진 벡터로 만듭니다.

쿼리와 문서의 벡터 가중치를 내적곱하기 때문에 쿼리와 문서에 같지만 뜻이 다른 토큰이 있다면 점수가 낮게 나올 것입니다.

하지만 이 방식은 너무 비싸고 기존 역색인 검색 방식에 잘 맞지 않았습니다.

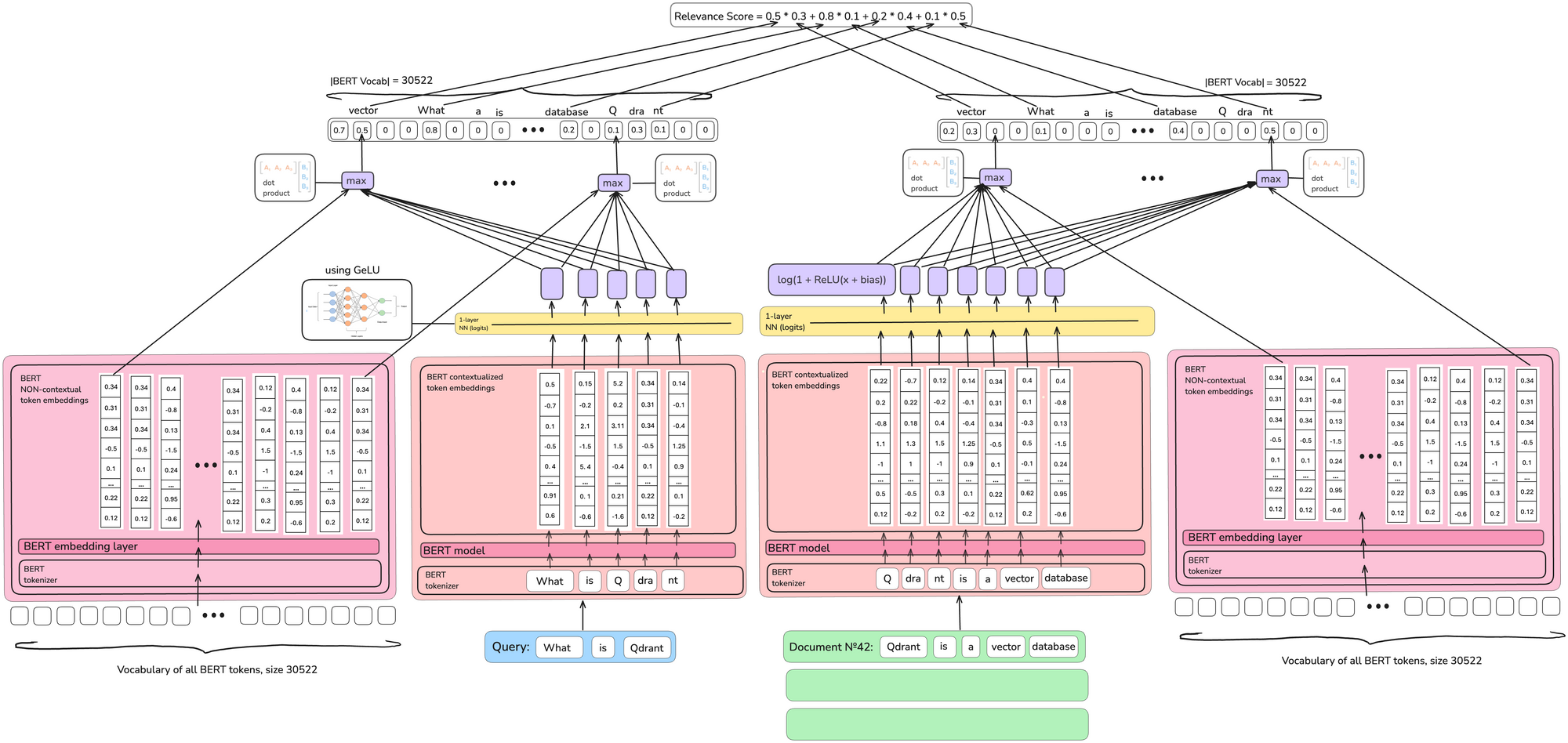
25년 5월 현재 가장 널리 쓰이는 모델은 SPLADE 입니다.

토큰마다 벡터를 가중치로 가지는 것은 비싸므로 다시 토큰은 하나의 스칼라 값을 가집니다.

다만 BERT의 모든 토큰 임베딩에 대해 dot product를 진행하여 0이 아닌 토큰 개수를 늘립니다. 이러면 비슷한 의미를 가진 토큰들이 sparse vector에 추가되므로 문서/쿼리가 확장되는 효과를 가집니다.

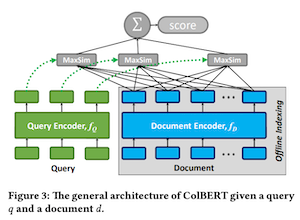
혹시 이전에 다루었던 ColBERT 가 기억나시나요? SPLADE와 비교하면 ColBERT는 정 반대의 모델입니다.

• SPLADE는 문서 하나를 하나의 벡터로 만듭니다.
• ColBERT는 문서 내 토큰 단위로 벡터를 만들어 문서 하나가 멀티 벡터입니다.
• SPLADE는 sparse vector이고 각 차원은 텀의 가중치에 대응됩니다.
• ColBERT는 문서와 쿼리 간 fine-grained, 토큰 레벨 interaction을 지향합니다.
• ColBERT의 벡터는 dense vector입니다.

ColBERT는 토큰 단위로 벡터를 만드므로 손실되는 정보가 적지만 SPLADE에 비해 상대적으로 비쌉니다.

두 방식이 가지는 장/단점이 있으므로 검색 서비스를 만들 때 서비스의 특성을 고려하여 사용하는 모델을 다르게 가져갑니다(당연히 ColBERT 외 다른 dense vector 모델을 사용하는 경우도 있습니다).

논문 살펴보기: Efficient Inverted Indexes for Approximate Retrieval over Learned Sparse Representations

Sparse vector 모델을 알아봤으니 이제 논문에서 제안하는 검색 엔진 구조를 살펴볼까요.

SPLADE를 서빙할 때 BM25와 같은 역색인 알고리즘을 서빙하는 검색엔진에 가중치 대신 sparse vector의 각 차원 값을 넣으면 쉽게 서빙을 할 수 있습니다.

이 논문에서는 LSR(Learned Sparse Retrieval)이 배운 가중치의 통계적인 성질은 역색인 기반 알고리즘이 동작하는 가정과 달라 기존 역색인 기반 검색엔진이 비효율적이라 말합니다.

• WAND나 MaxScore 같이 term frequency 모델 알고리즘은 쿼리가 짧고 term frequency가 Zipfian 분포를 보일 때 잘 작동합니다.
• 반면 LSR은 쿼리 길이가 길며 결정적으로 Zipfian 분포를 따르지 않아 쿼리당 응답 시간이 길어집니다.

WAND나 MaxScore은 검색 결과 set에 포함될 문서를 정할 때 문서의 점수를 전부 계산하지 않고 문서가 가질 수 있는 점수의 상한 값을 보고 점수를 계산할 문서의 후보 수를 줄입니다. 이런 최적화가 잘 작동하려면 역색인의 포스팅 리스트 길이가 Zipfian 분포를 따라야 하는데, sparse learned vector에서 sparsity가 차원에 대해 균일하여 효과적이지 않다는 것입니다.

이 논문이 제안한 구조는 역색인이 그래프 구조를 포함하고 있습니다. sparse embedding 서빙에서 ANN을 사용하는게 더 좋다고 판단한 것인데요. 실제로 2023 NeurlPS의 BigANN 챌린지 sparse embedding 트랙에서 dense 벡터용 그래프 베이스 ANN이 역색인 기반 구조들을 제치고 throughput top 2를 차지한 것에 영감을 받았습니다.

α-mass subvector

해당 논문을 살펴보기 전 알아야할 개념 중 α-mass subvector가 있습니다.

벡터 정규화 Lp를 다음과 같이 정의합니다.

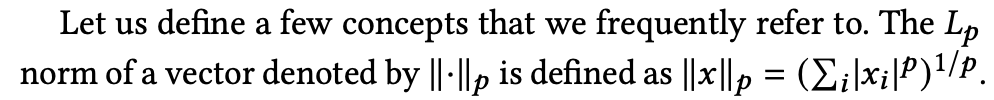
이 정규화 정의를 이용해 α-mass subvector를 정의합니다.

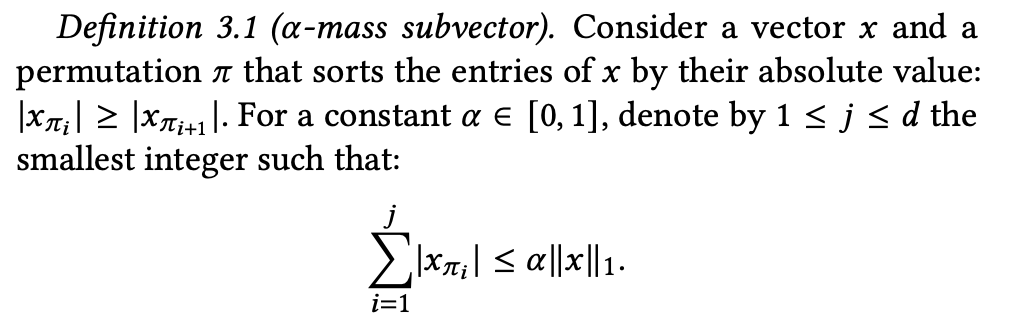
간단히 정리하면 벡터의 각 차원의 값을 내림차순 한 뒤 첫번째 값부터 j번째까지 더한 값이 “전체 차원의 값을 더한 값(L1) * α” 보다 작다면 이를 만족하는 벡터를 α-mass subvector라 합니다.

이 개념은 해당 논문이 제안한 알고리즘을 최적화할 때 사용합니다.

중요한 것에 집중한다

벡터의 L2 정규화에 많이 기여하는 차원 값은 벡터 사이의 dot product에도 영향을 많이 미칩니다. 이를 이용해 0이 아닌 값을 가진 차원에 대해 L2 mass에 비례하는 확률로 값을 버리면 벡터간 dot product 값을 거의 유지하면서 컬렉션 크기를 줄일 수 있습니다.

SPLADE, Efficient SPLADE도 비슷하게 벡터의 L1 mass에 비례하여 중요한 차원에만 집중하는 로직이 존재합니다. 논문에서 SPLADE로 벡터들을 임베딩한 후 alpha-mass subvector를 측정했는데, 쿼리는 top 10 엔트리들이 0.75 mass, 문서는 top 50이 0.75 mass subvector를 만듬을 확인했습니다.

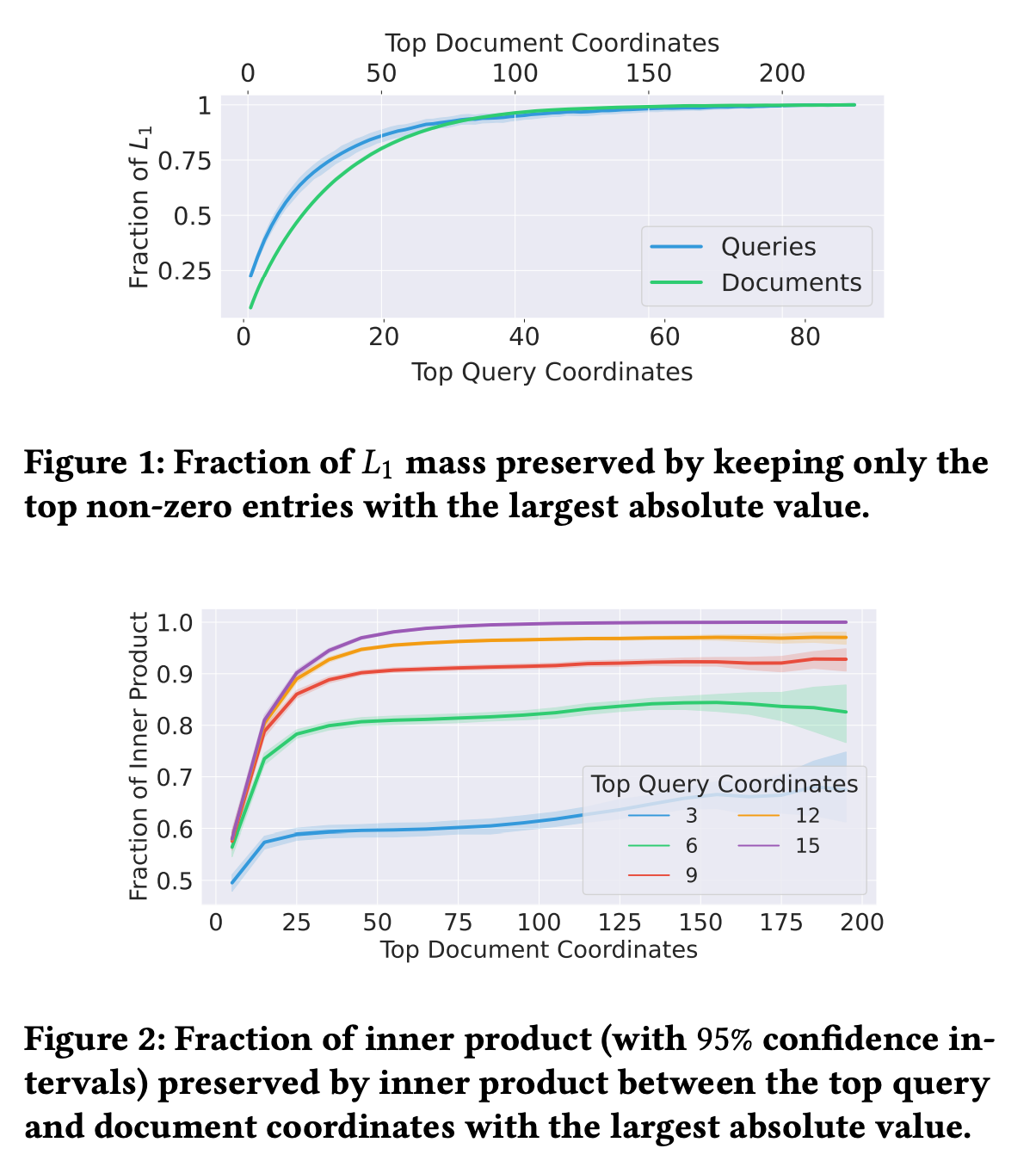
쿼리와 벡터 간 inner product도 비슷한 현상을 보입니다. Figure 2를 보면 쿼리와 문서의 좌표 값들 중 top 10%만을 가져와도 (쿼리 9, 문서 20) 85%의 full inner product를 계산할 수 있었습니다.

정리하면 LSR은 몇 개의 coordinate에 중요도가 몰려있고 값이 큰 엔트리들간 inner product이 전체 inner product의 값을 근사할 수 있습니다.

제안한 알고리즘: SEISMIC

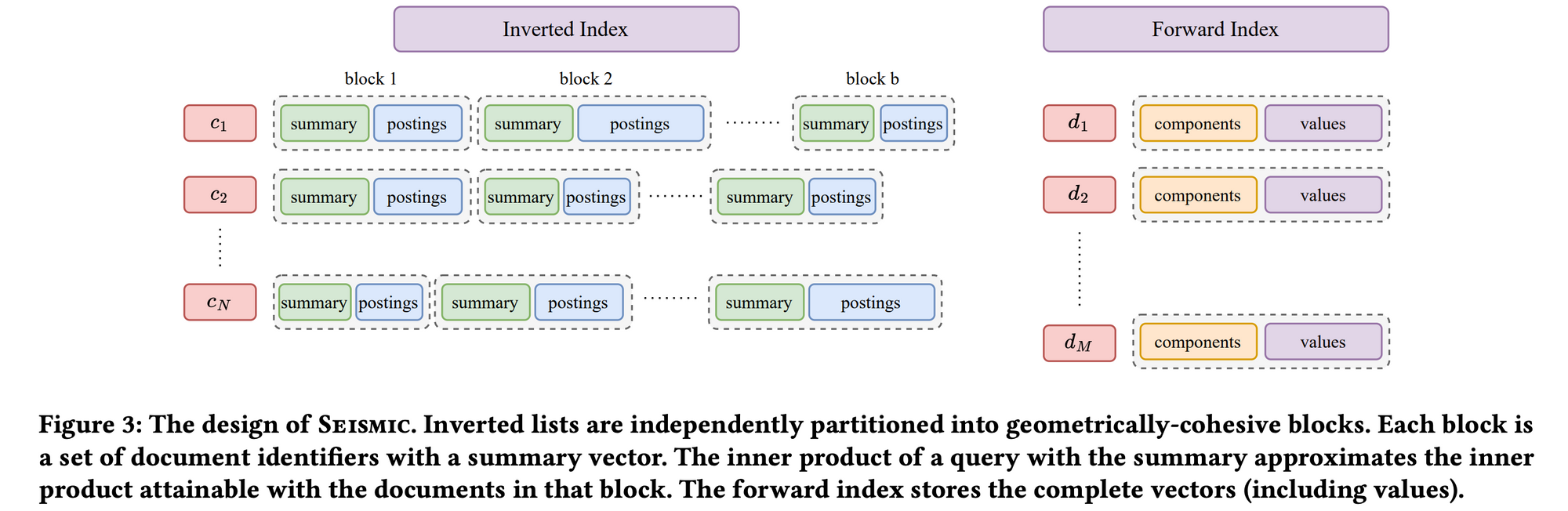
이 논문은 inverted index와 forward index를 둘 다 사용하는 SEISMIC 알고리즘을 제안합니다.

Inverted index는 문서들 중 평가할 문서 집합을 결정할 때 사용합니다.

Forward index는 평가 대상 문서의 inner production을 계산할 때 사용합니다.

(1) Inverted Index

저장하는 벡터의 개수: λ

앞서 보았듯 inner product의 값은 중요한 몇 개의 coordinate만을 계산하는 것으로 근사할 수 있습니다. SEISMIC은 이를 이용합니다.

벡터 내 각 원소를 순서대로 x1, x2, x3 … xn 이라고 합시다.

좌표 i에 대해 xi가 0이 아닌 벡터 x들을 모은 inverted list를 만듭니다. 이 inverted list를 li라고 합니다.

li는 xi의 값에 대해 내림차순으로 정렬되어 있습니다. 이때 모든 벡터를 다 저장하지 않고 최대  λ개까지 저장합니다. 이 λ는 하이퍼 파라미터로 관리합니다.

정리해보면 λ는 SEISMIC에서 static pruning을 조절하는 파라미터 역할을 하는 것입니다.

블록의 개수: β

SEISMIC은 dynamic pruning을 조절하는 하이퍼 파라미터도 가집니다.

각 inverted list는 β개의 작은 블록들로 나눠집니다. 이 β가 하이퍼 파라미터입니다.

SEISMIC은 클러스터링 알고리즘을 사용해 inverted list 내 존재하는 문서들을 β 개의 클러스터로 나눕니다. 각 클러스터 내 문서들의 id들이 블록을 구성하게 됩니다.

논문에서 클러스터링 알고리즘은 supervised, unsupervised 상관 없이 다 사용 가능하다고 합니다. 실험 시 사용한 알고리즘은 shallow K-Means입니다. 벡터 집합에서 랜덤하게 β 개의 벡터를 뽑고 이를 클러스터 대표 값으로 사용합니다. 그리고 모든 벡터에 대해 이 β 개의 벡터와 유사도를 계산하여 제일 큰 값을 보인 클러스터에 할당합니다.

summary 벡터 계산시 사용하는 벡터 개수: α

검색시 블록의 summary vector을 보고 해당 블록 내 문서들을 평가할지 말지 결정함으로써 SEISMIC은 dynamic pruning을 수행합니다.

summary vector는 블록 내 문서로부터 얻을 수 있는 inner product의 상한 값으로 정의됩니다. summary vector의 i번째 좌표는 블록 내 존재하는 문서들 중 최대 xi와 같습니다. summary vector와 inner product를 계산함으로써 해당 값이 일정 수준을 넘지 못하면 해당 블록 내 문서들을 스킵함으로써 검색 성능을 향상시키는 것입니다.

이 방법에서 주의할 점은 블록 사이즈가 커지면 summary 벡터 내 0이 아닌 엔트리 수가 증가한다는 것입니다. 그러면 summary 벡터를 저장하기 위한 공간 및 inner product 계산 시간이 커지게 됩니다.

그래서 summary 벡터 계산시 α mass subvector만 사용하여 계산합니다. 여기서 α는 SEISMIC에서 세번째이자 마지막 하이퍼파라미터로 사용됩니다.

추가적으로 논문에서는 스칼라 양자화를 적용해 summary vector 크기를 줄였습니다. 스칼라 양자화를 적용하면 벡터 내 각 좌표에 하나의 byte만 사용할 수 있습니다. 벡터 내 0이 아닌 값들 중 최소 값인 m을 0이 아닌 모든 좌표에 빼고 이를 sub interval로 나눕니다. 이때 최대 값은 255, 최소 값은 0이 되도록 sub interval을 정해야합니다. summary vector를 다시 복구할 때는 sub interval을 다시 곱하고 m을 더해 복구할 수 있습니다.

(2) Forward Index

Forward index는 정확한 문서 벡터를 살펴보기 위한 인덱스입니다. 쿼리와 블록 내 문서들과 inner product를 계산하기 위해 사용되며 블록이 평가 대상으로 선정되었을 때만 수행됩니다.

같은 블록 내 문서들이 forward index에 연속적으로 저장되는 것은 아닙니다. 같은 문서가 다른 inverted list에도 저장되기 때문입니다. 그래서 inner product 계산 시 많은 캐시 미스가 발생하고 레이턴시에도 영향을 미칩니다.

SEISMIC 알고리즘 정리

Inverted Index li 생성 과정

• d 차원의 벡터에 대해 d개의 inverted list 생성
• inverted list는 document id만 가지고 있고 d 좌표 값의 내림차순으로 정렬됨
• inverted list는 하이퍼 파라미터 λ 개의 문서만 저장
• 각 inverted list는 β 개의 블록들로 클러스터링
• 각 블록은 summary vector를 가짐
• summary vector 계산시 α mass subvector 사용

쿼리 처리 로직

• 쿼리 q에서 중요한 좌표를 뽑아낸다 (qcut)
• qcut의 각 좌표 i에 대해 summary를 사용해 블록을 평가한다.
• summary 추정 값이 min heap의 최소 inner product 보다 높으면 블록 내 문서들을 평가한다.
• inner product 계산 시 forward index를 사용해 문서의 완전한 벡터를 가져와 계산한다.

평가

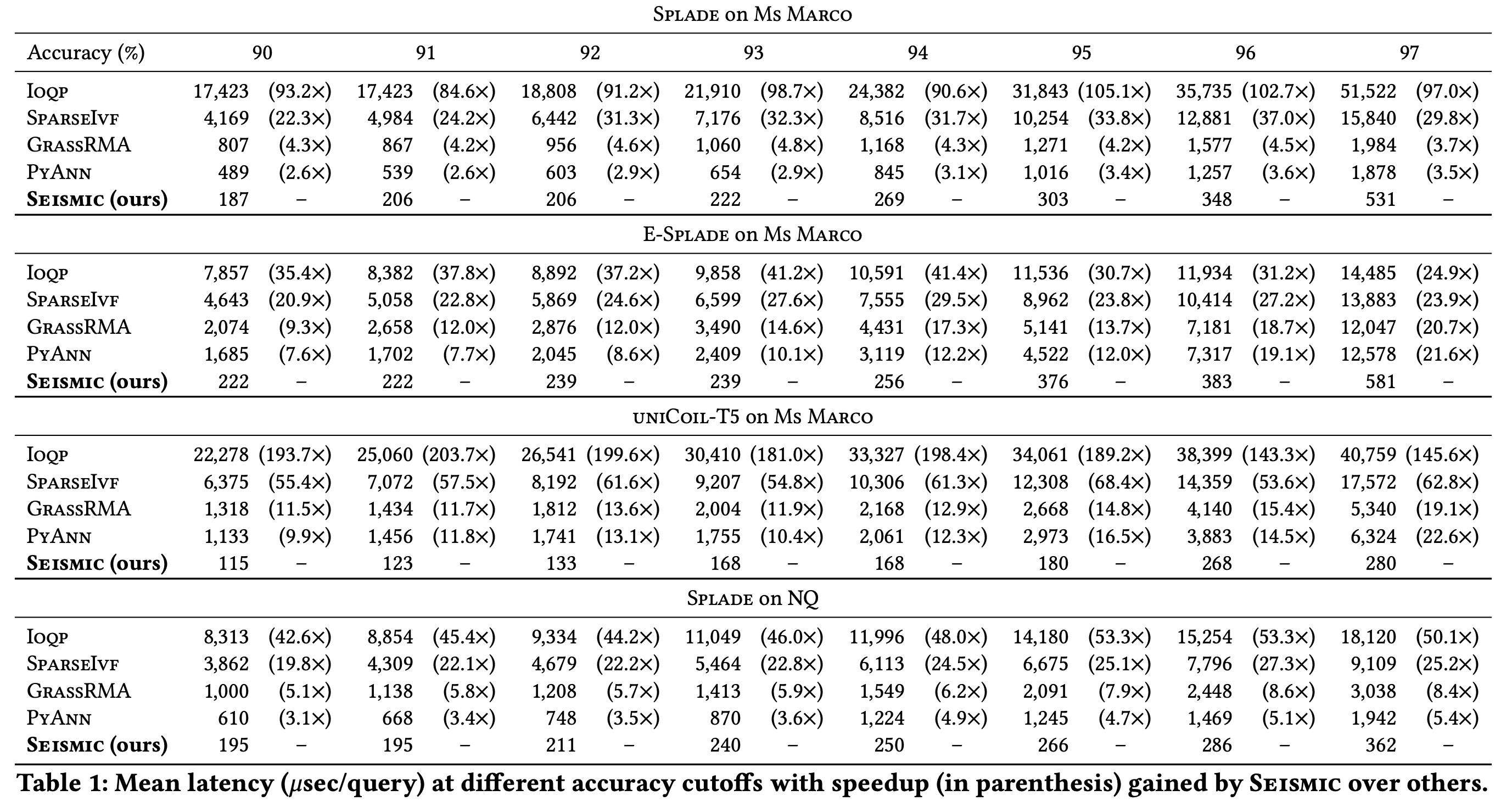
SEISMIC은 다른 알고리즘과 비교하여 동일한 정확도에서 훨씬 뛰어난 레이턴시를 보여주었습니다.

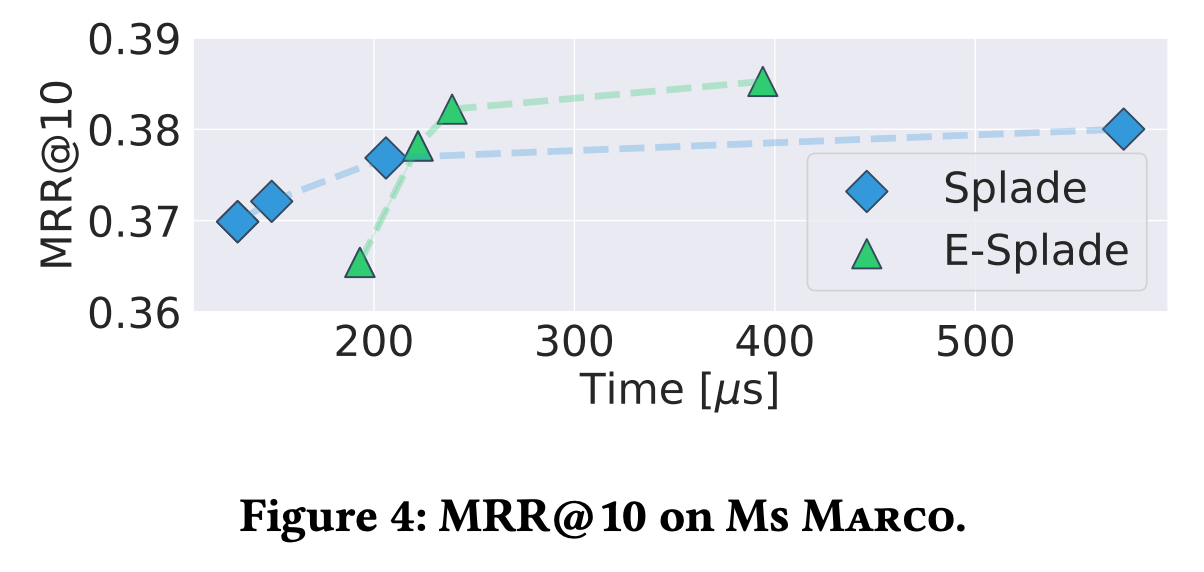
그동안 state-of-the-art 역색인 방식 솔루션들은 SPLADE를 사용할 때 충분히 빠르지 못하여 쿼리 처리 시간을 줄일 수 있는 E-SPLADE를 사용하였습니다. E-SPLADE를 사용하면 zero-shot 세팅일 때 SPLADE에 비하여 검색 품질(NDCG 등)이 좋지 않습니다.

SEISMIC은 SPLADE를 사용해도 쿼리 시간이 길지 않아 E-SPLADE로 넘어갈 필요가 없었습니다.

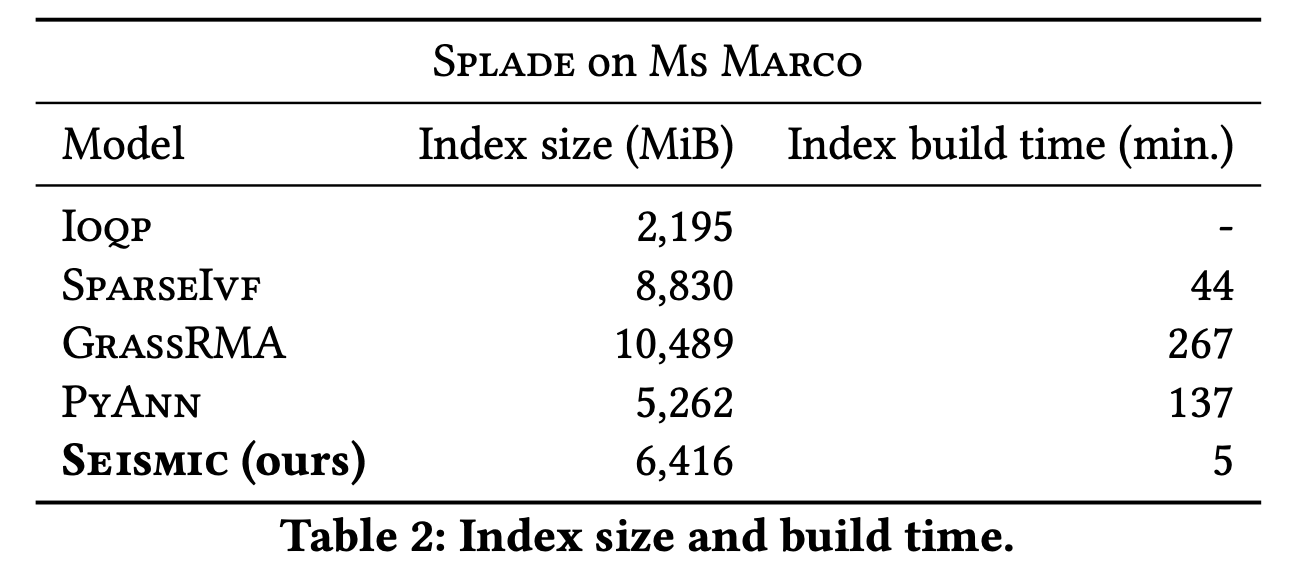
SEISMIC의 인덱스의 크기는 타 알고리즘 대비 양호한 편이고 빌드 시간은 다른 알고리즘과 비교해 훨씬 짧았습니다.

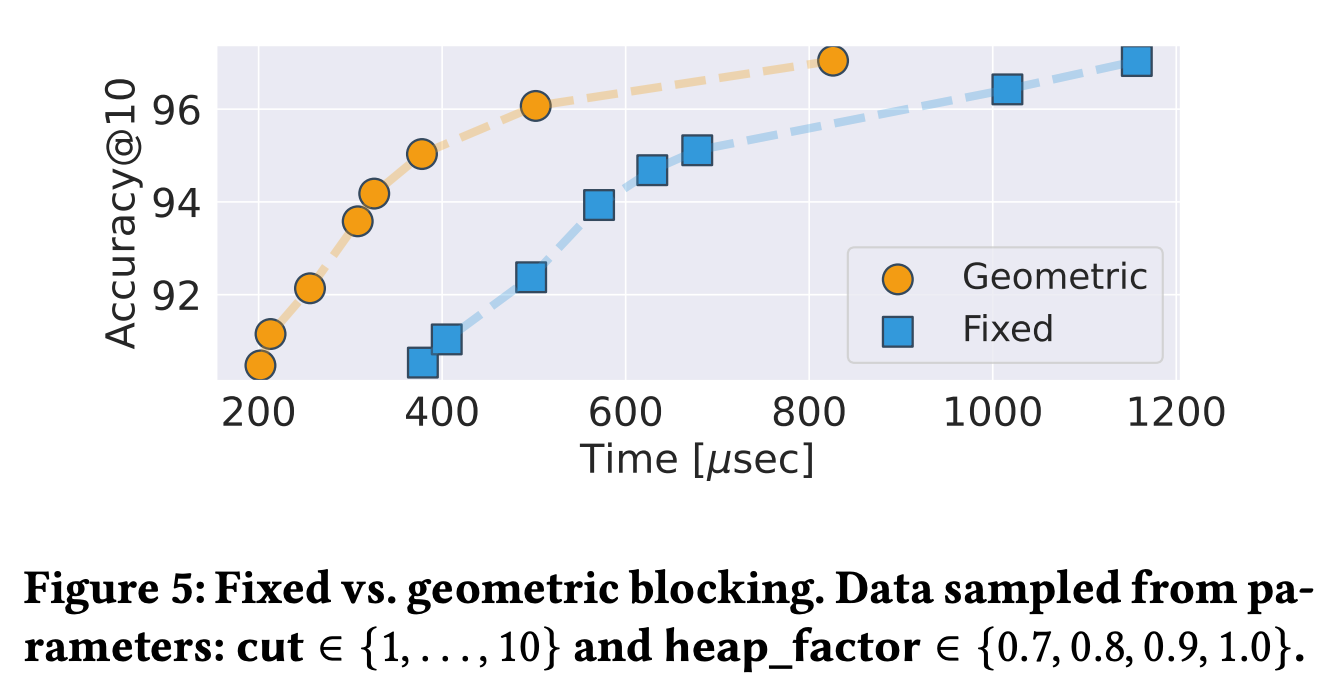
블록을 나눌 때 geometric(K-Means와 유사한 접근법)과 fixed(고정된 크기의 청크로 묶음)의 성능 차이를 보여줍니다. 클러스터링을 하는 것이 훨씬 성능이 좋은 것을 알 수 있습니다.

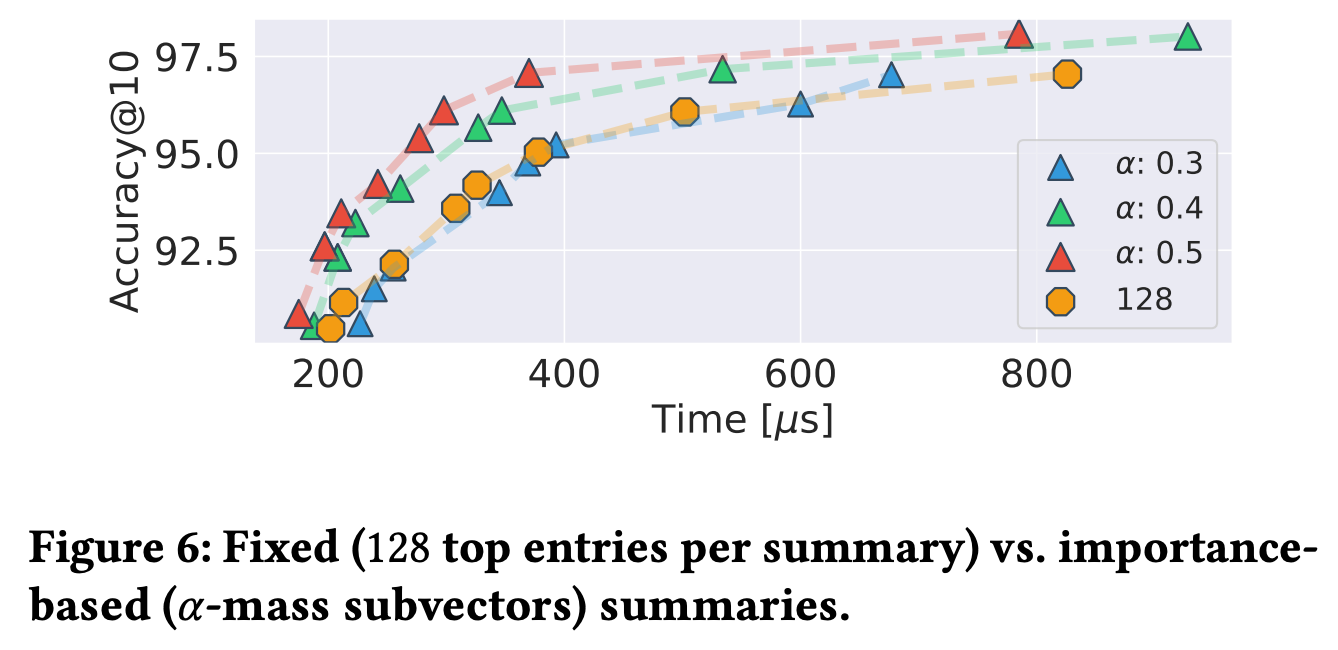
sumamry vector 계산시 고정된 개수의 엔트리로 계산하는 것과 중요도 기준인 α mass subvector로 계산할 때의 성능 차이를 보여줍니다. α mass subvector로 계산할 때 동일한 정확도 기준시 성능이 훨씬 좋았습니다.

마무리

이번 글에서 검색시 sparse vector를 사용하는 이유와 역색인 검색 엔진 구조에서 sparse vector를 서빙하는 새로운 알고리즘인 SEISMIC 을 살펴 보았습니다.

제안된 SEISMIC을 다음의 이유 때문에 바로 실서비스 검색엔진에 적용하기는 어려워 보입니다. 하지만 충분히 해결 가능한 문제들이라 좀 더 고민해보면 SEISMIC을 적용한 검색엔진이 등장할 수 있을 것 같습니다.

1. 실서비스 검색엔진은 실시간으로 벡터 입력을 계속 받습니다. SEISMIC은 블록의 개수를 β 개로 고정하기 때문에 시간이 지날수록 블록이 계속 커져 효율이 떨어질 수 있습니다. 일정 크기 이상이 되면 블록을 나누는 등의 알고리즘이 추가로 필요할 것 같습니다.
2. 검색 엔진이 벡터 삭제/수정 기능을 지원하면 벡터 삭제/수정시 summary vector를 수정할지 결정하는 알고리즘이 필요합니다.

개인적으로 역색인 구조에 클러스터링 알고리즘을 합친 것과 inner product의 값은 중요한 몇 개의 좌표에 영향을 크게 받는 것을 이용한 α mass subvector 최적화가 흥미로웠습니다. 검색 엔진을 만들고 있는 입장에서 해당 아이디어는 현업에서 사용할 수 있는 유용한 아이디어라고 생각합니다.

Reference

Efficient Inverted Indexes for Approximate Retrieval over Learned Sparse Representations

Modern Sparse Neural Retrieval: From Theory to Practice